1. Производная логарифмической функции Сначала рассмотрим частный случай




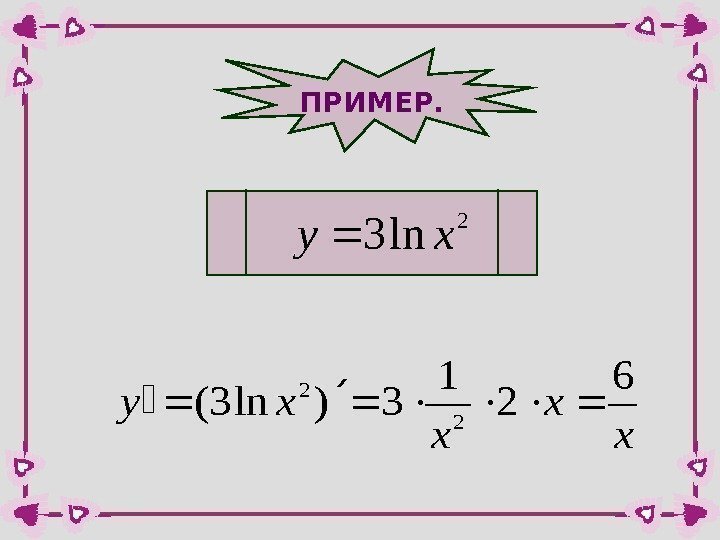









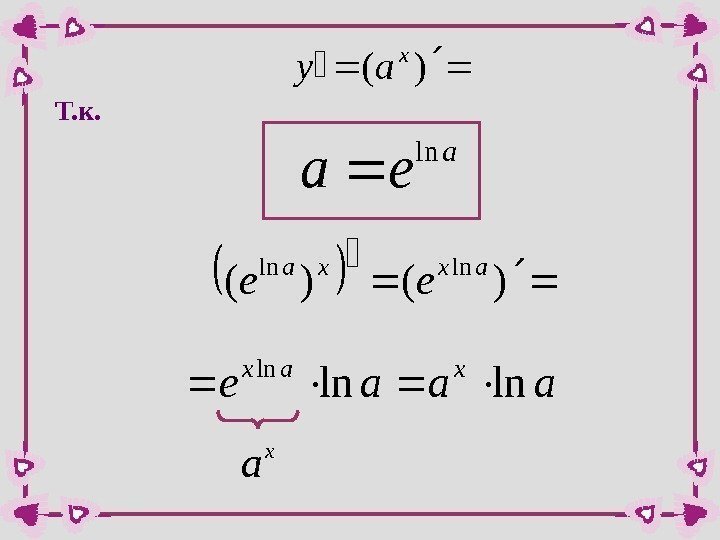






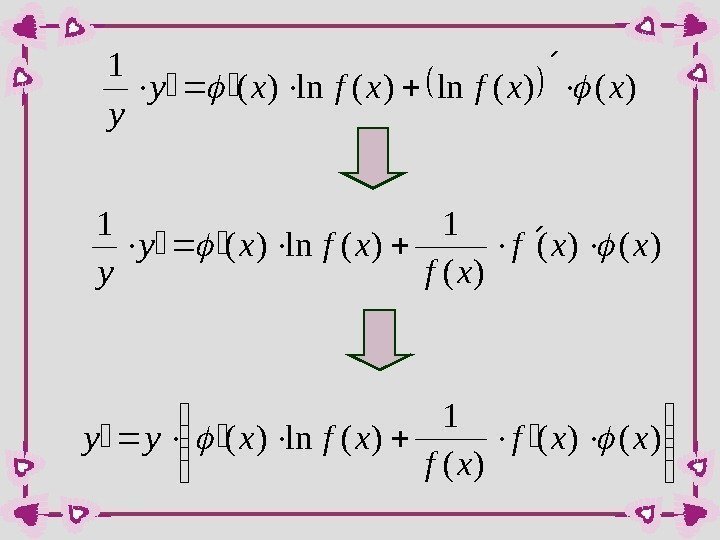











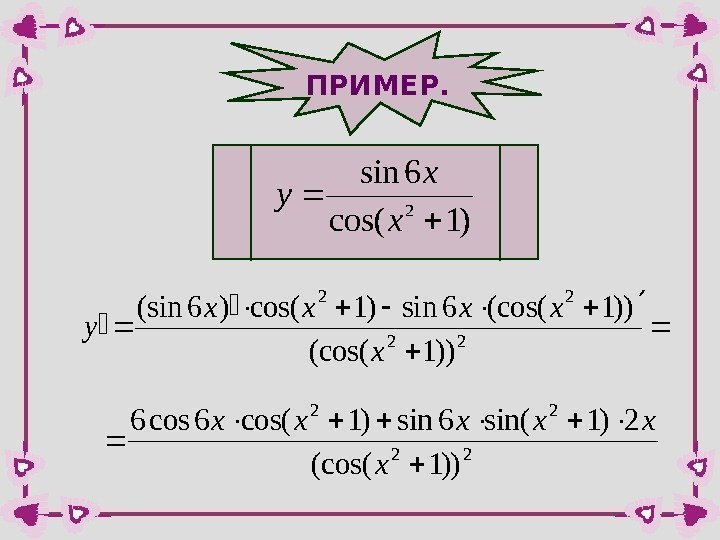









8.6..ppt
- Размер: 677.0 Кб
- Автор:
- Количество слайдов: 55
Описание презентации 1. Производная логарифмической функции Сначала рассмотрим частный случай по слайдам
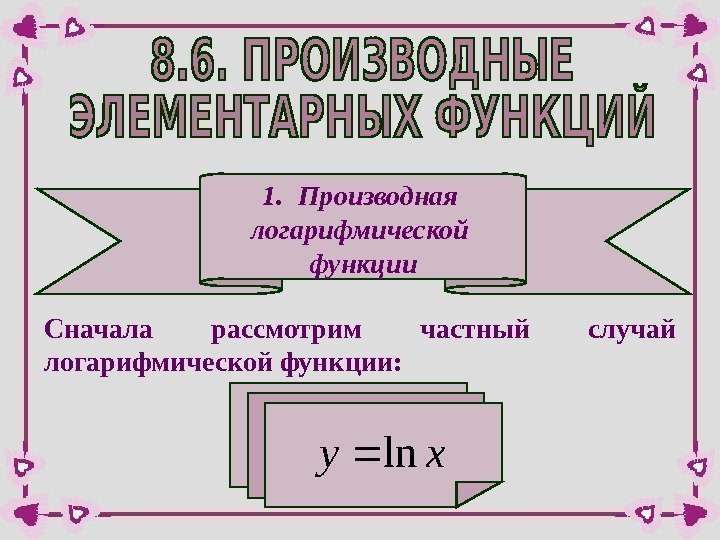
 1. Производная логарифмической функции Сначала рассмотрим частный случай логарифмической функции: xyln
1. Производная логарифмической функции Сначала рассмотрим частный случай логарифмической функции: xyln
 Дадим аргументу х приращение Δ х и найдем значение функции y+ Δ y : )ln(xxyy Находим приращение функции xxxy ln)ln(Используем схему нахождения производной: По свойству логарифма: x xx 1 lnln
Дадим аргументу х приращение Δ х и найдем значение функции y+ Δ y : )ln(xxyy Находим приращение функции xxxy ln)ln(Используем схему нахождения производной: По свойству логарифма: x xx 1 lnln
 Составляем отношение x x xx y 1 ln 1 Находим предел этого отношения: x x xx y y xx 1 ln 1 limlim 00 Сделаем замену: xyxy x x ;
Составляем отношение x x xx y 1 ln 1 Находим предел этого отношения: x x xx y y xx 1 ln 1 limlim 00 Сделаем замену: xyxy x x ;
 Тогда y xyy 1 ln 1 lim 0 y y y x 1 0 1 ln 1 lim y y y x 1 0 1 lnlim 1 x e x y y 1 ln 1 1 limln 11 0 e 1 В силу непрерывности логарифмической функции меняем местами знаки логарифма и предела:
Тогда y xyy 1 ln 1 lim 0 y y y x 1 0 1 ln 1 lim y y y x 1 0 1 lnlim 1 x e x y y 1 ln 1 1 limln 11 0 e 1 В силу непрерывности логарифмической функции меняем местами знаки логарифма и предела:
 x x 1 )(ln. Для сложной функции: u u u 1 )(ln
x x 1 )(ln. Для сложной функции: u u u 1 )(ln
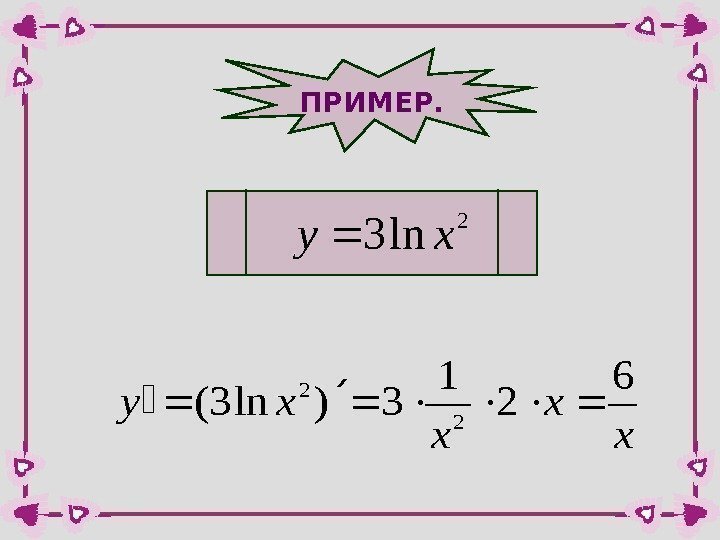 ПРИМЕР. 2 ln 3 xy x xy 6 2 1 3)ln 3(
ПРИМЕР. 2 ln 3 xy x xy 6 2 1 3)ln 3(
 Найдем производную для общего случая логарифмической функции: xy a log
Найдем производную для общего случая логарифмической функции: xy a log
 По свойству логарифмаa x xa ln ln log Тогда a x xya ln ln )(log ax x aln 1 )(ln ln 1 x 1 Отсюда окончательно имеем
По свойству логарифмаa x xa ln ln log Тогда a x xya ln ln )(log ax x aln 1 )(ln ln 1 x 1 Отсюда окончательно имеем
 ax xa ln 1 )(log Для сложной функции: u au ua ln 1 )(log
ax xa ln 1 )(log Для сложной функции: u au ua ln 1 )(log
 ПРИМЕР. )3(log 2 5 xxy )32( 5 ln 1 3 1 ))3((log 2 2 5 x xx xxy
ПРИМЕР. )3(log 2 5 xxy )32( 5 ln 1 3 1 ))3((log 2 2 5 x xx xxy
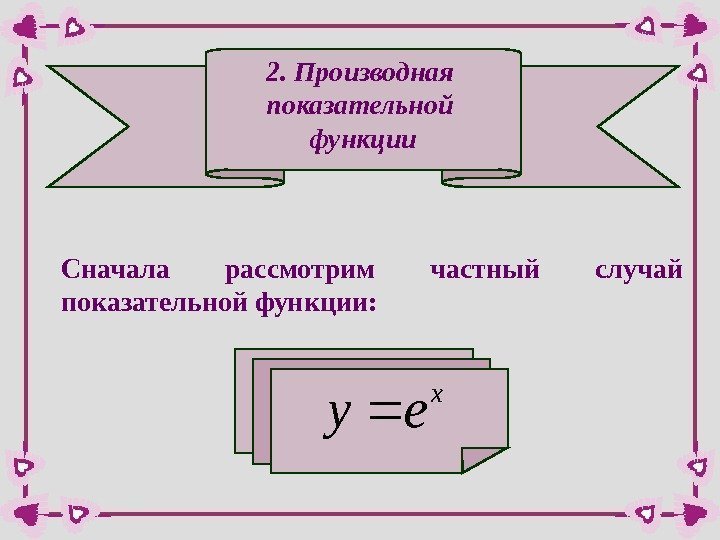
 2. Производная показательной функции Сначала рассмотрим частный случай показательной функции: x ey
2. Производная показательной функции Сначала рассмотрим частный случай показательной функции: x ey
 Логарифмируем обе части равенства по основанию e : xexey x lnlnln Дифференцируем обе части равенства по х : xy)(ln 1 1 y y Отсюда выражаем искомую производную: yy Т. к. x ey то окончательно получаем: x ey
Логарифмируем обе части равенства по основанию e : xexey x lnlnln Дифференцируем обе части равенства по х : xy)(ln 1 1 y y Отсюда выражаем искомую производную: yy Т. к. x ey то окончательно получаем: x ey
 xx ee)(Для сложной функции: uee uu )(
xx ee)(Для сложной функции: uee uu )(
 Кривая x ey (экспонента) обладает свойством: в каждой точке х ордината у равна угловому коэффициенту касательной к кривой в этой точке : tge x
Кривая x ey (экспонента) обладает свойством: в каждой точке х ордината у равна угловому коэффициенту касательной к кривой в этой точке : tge x
 ПРИМЕР. x exy 5 )51(5)( 5555 xeexeexy xxxx
ПРИМЕР. x exy 5 )51(5)( 5555 xeexeexy xxxx
 Найдем производную для общего случая показательной функции: x ay
Найдем производную для общего случая показательной функции: x ay
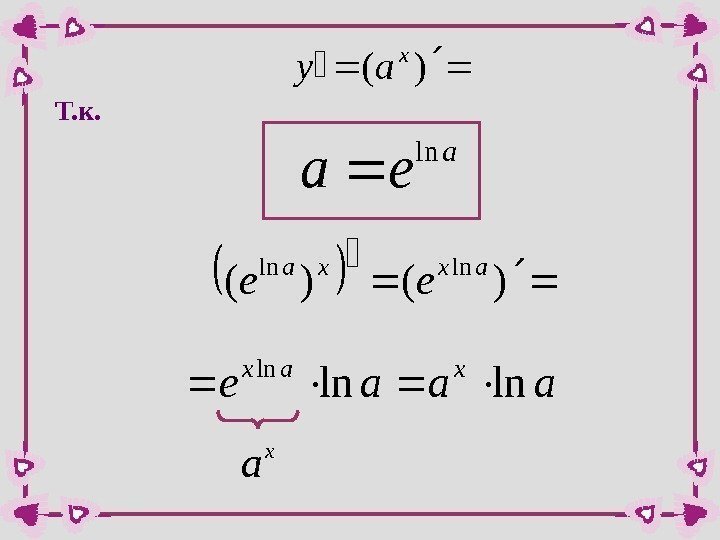 )( x ay. Т. к. a ealn )()( lnlnaxxa ee aaae xax lnln ln x a
)( x ay. Т. к. a ealn )()( lnlnaxxa ee aaae xax lnln ln x a
 aaa xx ln)(Для сложной функции: uaaa uu ln)(
aaa xx ln)(Для сложной функции: uaaa uu ln)(
 ПРИМЕР. xxy 33 7 xxy xxxx 333 37 ln 7)7( 33 )19(7 ln 7 233 x xx
ПРИМЕР. xxy 33 7 xxy xxxx 333 37 ln 7)7( 33 )19(7 ln 7 233 x xx
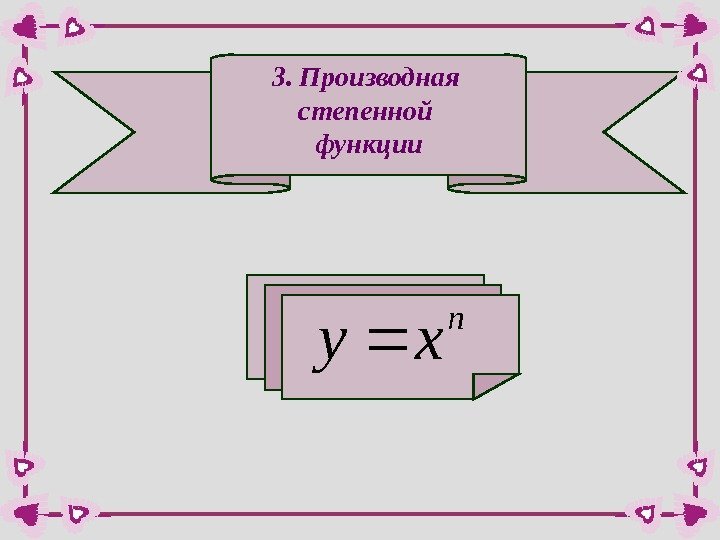
 3. Производная степенной функцииn xy
3. Производная степенной функцииn xy
 Логарифмируем обе части равенства по основанию e : xnxy n lnlnln Дифференцируем обе части равенства по х : )ln()(lnxny x ny y
Логарифмируем обе части равенства по основанию e : xnxy n lnlnln Дифференцируем обе части равенства по х : )ln()(lnxny x ny y
 Отсюда выражаем искомую производную: x nyy 1 Т. к. n xy то окончательно получаем: 11 nn xn x xny
Отсюда выражаем искомую производную: x nyy 1 Т. к. n xy то окончательно получаем: 11 nn xn x xny
 1 )( nn xnx. Для сложной функции: uunu nn 1 )(
1 )( nn xnx. Для сложной функции: uunu nn 1 )(
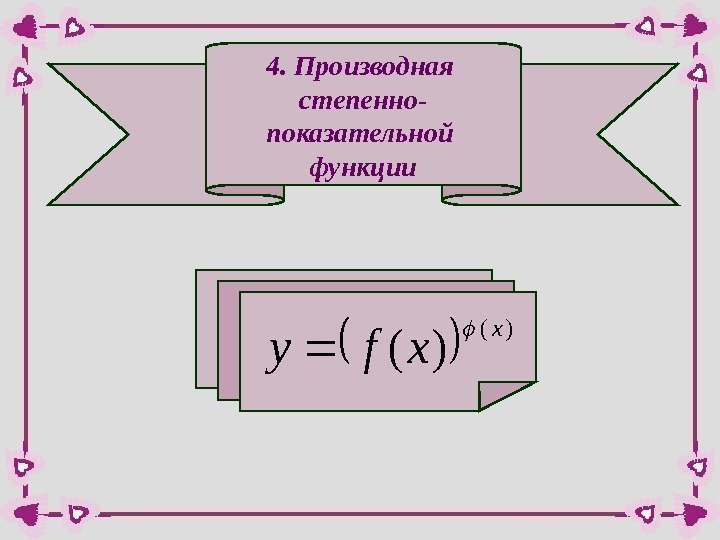
 4. Производная степенно- показательной функции )( )( x xfy
4. Производная степенно- показательной функции )( )( x xfy
 Логарифмируем обе части равенства по основанию e : )(ln)()(lnln )( xfxxfy x Дифференцируем обе части равенства по х, учитывая, что в правой части стоит произведение: )(ln)()(lnxfxy
Логарифмируем обе части равенства по основанию e : )(ln)()(lnln )( xfxxfy x Дифференцируем обе части равенства по х, учитывая, что в правой части стоит произведение: )(ln)()(lnxfxy
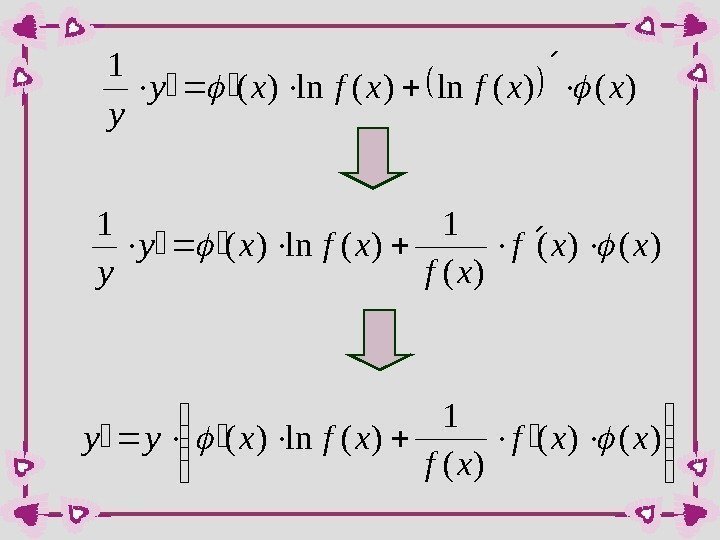 )()(ln)( 1 xxfxfxy y )()( )( 1 )(ln)( 1 xxf xf xfxy y )()( )( 1 )(ln)(xxf xf xfxyy
)()(ln)( 1 xxfxfxy y )()( )( 1 )(ln)( 1 xxf xf xfxy y )()( )( 1 )(ln)(xxf xf xfxyy
 Т. к. то окончательно получаем: )( )( x xfy )()( )( 1 )(ln)()( )( xxf xf xfxxfy x )()(ln)()( 1)()( xxfxfxfxxf xx
Т. к. то окончательно получаем: )( )( x xfy )()( )( 1 )(ln)()( )( xxf xf xfxxfy x )()(ln)()( 1)()( xxfxfxfxxf xx
 Чтобы продифференцировать степенно-показательную функцию, ее сначала нужно продифференцировать как показательную функцию, а затем как степенную и полученные результаты сложить.
Чтобы продифференцировать степенно-показательную функцию, ее сначала нужно продифференцировать как показательную функцию, а затем как степенную и полученные результаты сложить.
 ПРИМЕР. x xy )ln 1(ln)( 1 xxxxxxxy xxnx
ПРИМЕР. x xy )ln 1(ln)( 1 xxxxxxxy xxnx
 ЗАМЕЧАНИЕ Производная логарифмической функцииy y y 1 )(ln называется логарифмической производной. Ее удобно использовать для дифференцирования функции, выражение которой существенно упрощается при логарифмирования.
ЗАМЕЧАНИЕ Производная логарифмической функцииy y y 1 )(ln называется логарифмической производной. Ее удобно использовать для дифференцирования функции, выражение которой существенно упрощается при логарифмирования.
 ПРИМЕР. x xx y 3 )2)(1(
ПРИМЕР. x xx y 3 )2)(1(
 Логарифмируем обе части равенства по основанию e : x xx y 3 )2)(1( lnln 2 Используем свойства логарифма: x xx 3 )2)(1( ln 2 1 2 )3 ln()2 ln()1 ln( 2 12 xxx
Логарифмируем обе части равенства по основанию e : x xx y 3 )2)(1( lnln 2 Используем свойства логарифма: x xx 3 )2)(1( ln 2 1 2 )3 ln()2 ln()1 ln( 2 12 xxx
 Дифференцируем обе части равенства по х : )3 ln()2 ln()1 ln( 2 1 )(ln 2 xxxy xx x x y y 3 1 2 2 1 1 2 11 2 x xx xx x x y 3 )2)(1(
Дифференцируем обе части равенства по х : )3 ln()2 ln()1 ln( 2 1 )(ln 2 xxxy xx x x y y 3 1 2 2 1 1 2 11 2 x xx xx x x y 3 )2)(1(
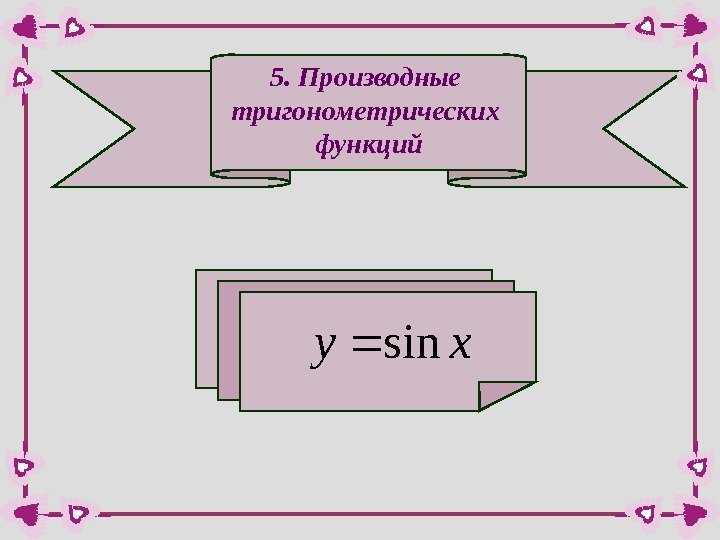
 5. Производные тригонометрических функцийxysin
5. Производные тригонометрических функцийxysin
 Дадим аргументу х приращение Δ х и найдем значение функции y+ Δ y : )sin(xxyy Находим приращение функции xxxysin)sin(Используем схему нахождения производной: Распишем разность синусов: 2 cos 2 sin 2 x x x
Дадим аргументу х приращение Δ х и найдем значение функции y+ Δ y : )sin(xxyy Находим приращение функции xxxysin)sin(Используем схему нахождения производной: Распишем разность синусов: 2 cos 2 sin 2 x x x
 Составляем отношение Находим предел этого отношения: x x x y 2 cos 2 sin 2 x x x y y xx 2 cos 2 sin 2 limlim
Составляем отношение Находим предел этого отношения: x x x y 2 cos 2 sin 2 x x x y y xx 2 cos 2 sin 2 limlim
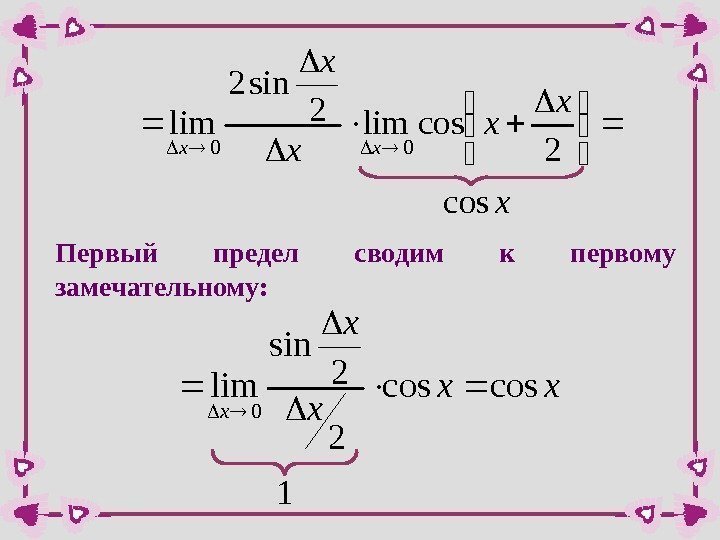
 2 coslim 2 sin 2 lim 00 x x xx xcos. Первый предел сводим к первому замечательному: xx x coscos 2 2 sin lim
2 coslim 2 sin 2 lim 00 x x xx xcos. Первый предел сводим к первому замечательному: xx x coscos 2 2 sin lim
 xxcos)(sin. Для сложной функции: uuucos)(sin
xxcos)(sin. Для сложной функции: uuucos)(sin
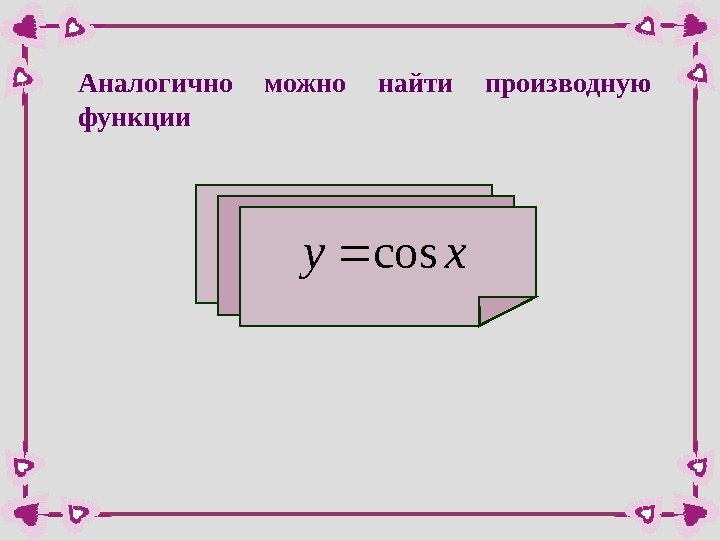
 Аналогично можно найти производную функцииxycos
Аналогично можно найти производную функцииxycos
 xxsin)(cos. Для сложной функции: uuusin)(cos
xxsin)(cos. Для сложной функции: uuusin)(cos
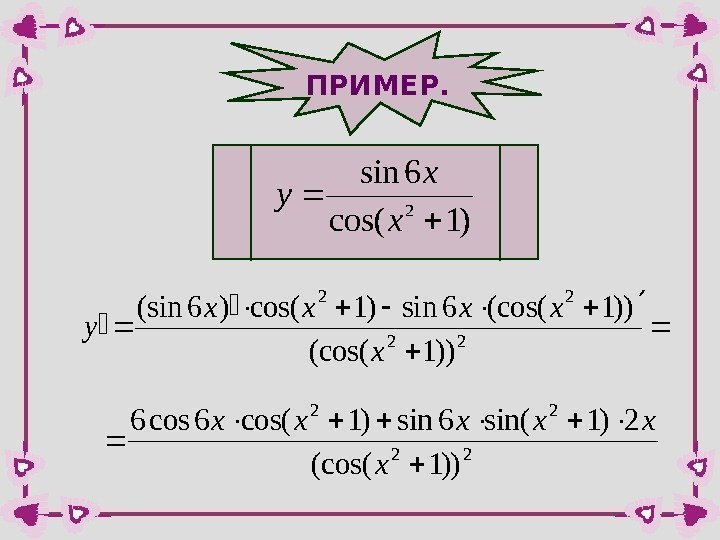 ПРИМЕР. )1 cos( 6 sin 2 x x y 22 22 ))1(cos(6 sin)1 cos()6(sin x xxxx y 22 22 ))1(cos( 2)1 sin(6 sin)1 cos(6 cos 6 x xxxxx
ПРИМЕР. )1 cos( 6 sin 2 x x y 22 22 ))1(cos(6 sin)1 cos()6(sin x xxxx y 22 22 ))1(cos( 2)1 sin(6 sin)1 cos(6 cos 6 x xxxxx
 Найдем производную функцииtgxy
Найдем производную функцииtgxy
 Находим производную дроби: x x tgxy cos sin )( x xxxx 2 cos )(cossincos)(sin xx xx 22 22 cos 1 cos sincos
Находим производную дроби: x x tgxy cos sin )( x xxxx 2 cos )(cossincos)(sin xx xx 22 22 cos 1 cos sincos
 x tgx 2 cos 1 )( Для сложной функции: u u tgu 2 cos 1 )(
x tgx 2 cos 1 )( Для сложной функции: u u tgu 2 cos 1 )(
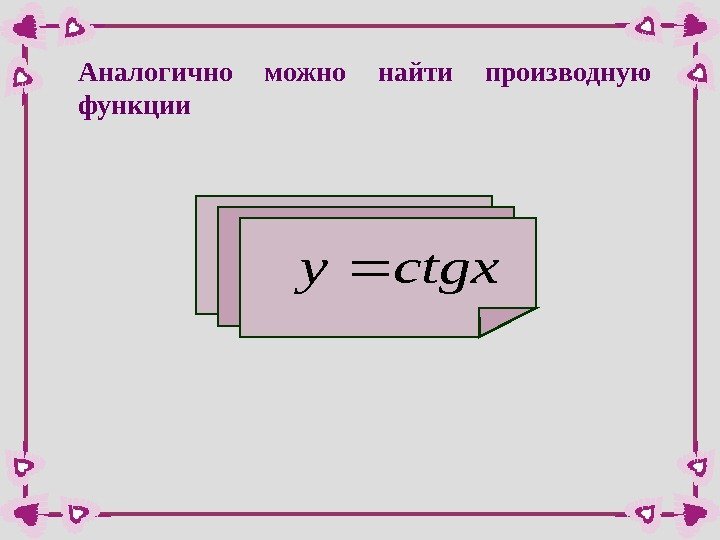
 Аналогично можно найти производную функцииctgxy
Аналогично можно найти производную функцииctgxy
 x ctgx 2 sin 1 )(Для сложной функции: u u ctgu 2 sin 1 )(
x ctgx 2 sin 1 )(Для сложной функции: u u ctgu 2 sin 1 )(
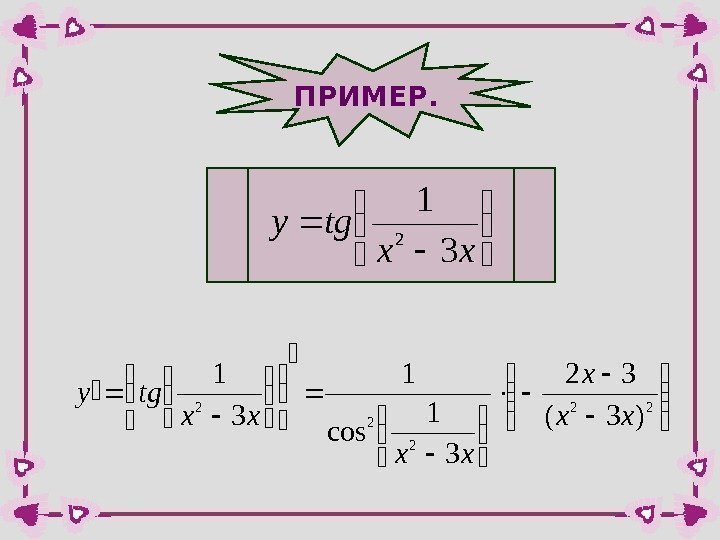
 ПРИМЕР. xxtgy 31 2 22 2 )3( 32 3 1 cos 1 3 1 xx xx tgy
ПРИМЕР. xxtgy 31 2 22 2 )3( 32 3 1 cos 1 3 1 xx xx tgy
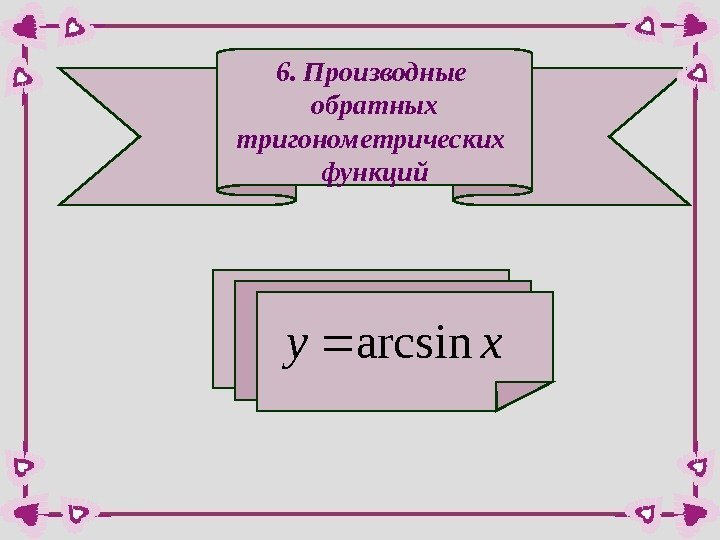
 6. Производные обратных тригонометрических функцийxyarcsin
6. Производные обратных тригонометрических функцийxyarcsin
 Обратной к ней функцией будетyxsin Используем правило дифференцирования обратной функции: x y y x 1 yx y y x cos 11 Теперь нужно выразить у через х с помощью основного тригонометрического соотношения: 22 1 1 sin 1 1 cos 1 )(arcsin xyy x 2 x Эта производная не существует при 1 x
Обратной к ней функцией будетyxsin Используем правило дифференцирования обратной функции: x y y x 1 yx y y x cos 11 Теперь нужно выразить у через х с помощью основного тригонометрического соотношения: 22 1 1 sin 1 1 cos 1 )(arcsin xyy x 2 x Эта производная не существует при 1 x
 2 1 1 )(arcsin x x Для сложной функции: u u u 2 1 1 )(arcsin
2 1 1 )(arcsin x x Для сложной функции: u u u 2 1 1 )(arcsin
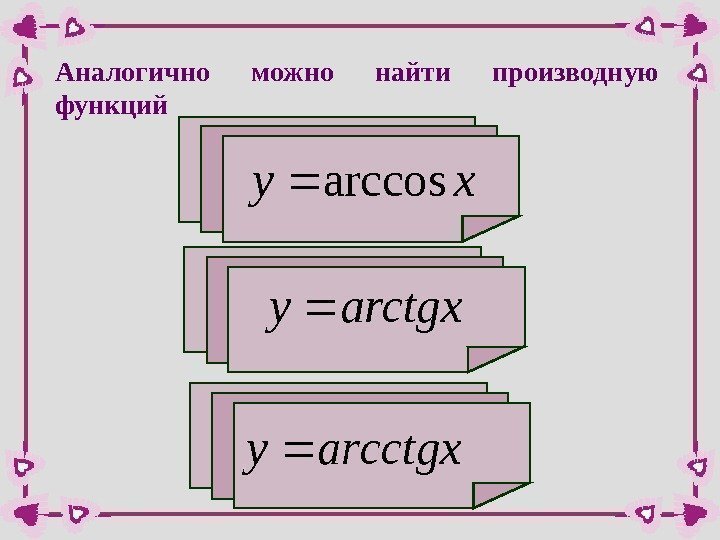
 Аналогично можно найти производную функцийxyarccos arctgxy arcctgxy
Аналогично можно найти производную функцийxyarccos arctgxy arcctgxy
 2 1 1 )(arccos x x Для сложной функции: u u u 2 1 1 )(arccos
2 1 1 )(arccos x x Для сложной функции: u u u 2 1 1 )(arccos
 2 1 1 )( x arctgx Для сложной функции: u u arctgu 2 1 1 )(
2 1 1 )( x arctgx Для сложной функции: u u arctgu 2 1 1 )(
 2 1 1 )( x arcctgx Для сложной функции: u u arcctgu 2 1 1 )(
2 1 1 )( x arcctgx Для сложной функции: u u arcctgu 2 1 1 )(
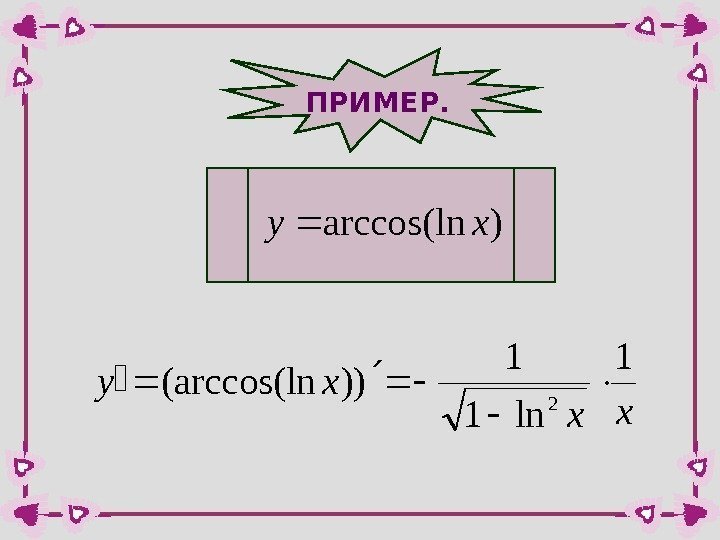
 ПРИМЕР. )arccos(lnxy xx xy 1 ln 1 1 ))(arccos(ln
ПРИМЕР. )arccos(lnxy xx xy 1 ln 1 1 ))(arccos(ln
