1 Приклади автоматів Лекція 12 2 Приклади автоматів

1 Приклади автоматів Лекція 12

2 Приклади автоматів Приклад 4.1. (1) Приклад 4.1. Задано абстрактний автомат A = , де X = {x1, x2, x3}, Q = {q1, q2, q3, q4}, Y = {y1, y2}, а відображення :Q  XQ і :QXY визначаються таким чином (таблиці для задання функцій (q, x) і (q, x) поєднано): Fq1 = {q2(x1/y1), q4(x2/y1), q1(x3/y2)}, Fq2 = {q1(x1/y2), q3(x2/y1), q4(x3/y1)}, Fq3 = {q1(x1/y1), q4(x2/y2), q2(x3/y2)}, Fq4 = {q4(x1/y2), q1(x2/y1), q3(x3/y1)}.

3 Сформуємо таблиці переходів  та виходів : Припустимо, що скінченний автомат A є автоматом першого роду. При подачі на вхід скінченного автомата A, який встановлено у початковий стан q1 вхідного слова p1 = x1x1x2x3x2x3, на виході з'явиться слово r1 = y1y2y1y1y2y1, а вхідне слово p2 = x3x2x2x1x1x3x1x2 спричинить появу вихідного слова r2 = y2y1y1y1y2y2y1y1. Приклад 4.1. (2) Приклади автоматів

4 Приклади автоматів Ґрунтуючись на відображеннях  і , легко побудувати таблиці переходів і виходів скінченного автомата A. Таблицю переходів, що визначає функцію переходів (q, x), і таблицю виходів, що визначає звичайну функцію виходів (q, x), наведено вище. Графоїд скінченного автомата A та його матрицю з'єднань R зображено на слайді 5. Нижні три яруси навантаженого прадерева, що побудоване за графоїдом скінченного автомата A, подано на слайді 6. Приклад 4.1. (3)

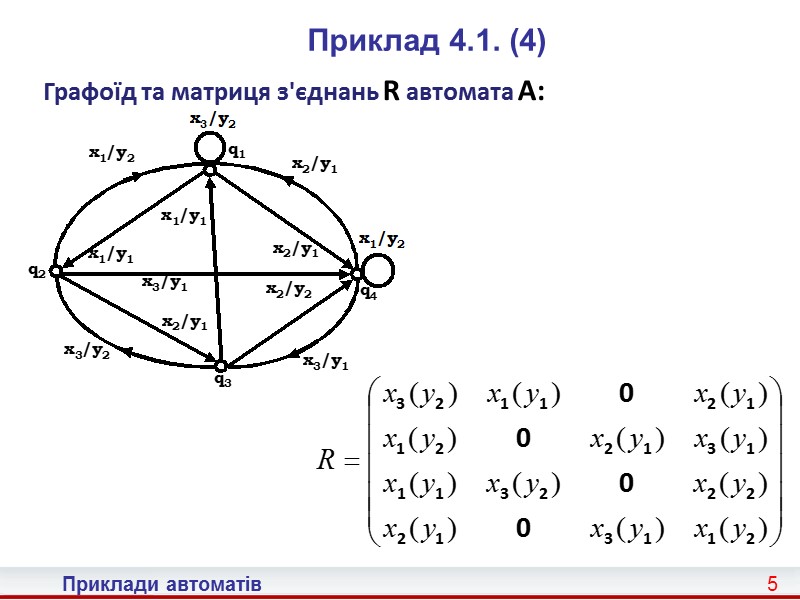
5 Приклади автоматів Приклад 4.1. (4) Графоїд та матриця з'єднань R автомата A:

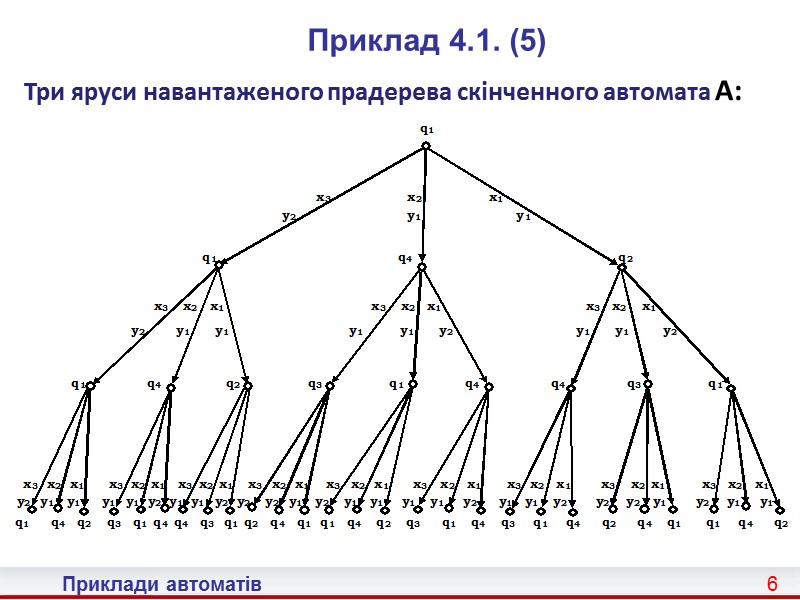
6 Приклади автоматів Приклад 4.1. (5) Три яруси навантаженого прадерева скінченного автомата A:

7 Приклади автоматів Приклад 4.2. (1) Далі вважатимемо, що скінченний автомат A є автоматом другого роду. Тоді, як і раніше, наведені вище таблиці задають функцію переходів (q, x) і зсунуту функцію виходів (q, x) автомата A. Графоїд автомата другого роду і матрицю з'єднань показано на слайді 5. Якщо на вхід скінченного автомата A, встановленого у початковий стан q1, подати вхідні слова p1=x1x1x2x3x2x3 і p2 = x3x2x2x1x1x3x1x2 такі самі, як й у випадку автомата першого роду, то на виході одержимо слова r1 = y2y1y1y2y1y2 і r2 = y2y1y1y2y1y2y2y2, відмінні від вихідних слів автомата першого роду. Тому відображення f, що індукує абстрактний автомат A першого роду, відрізняється від відображення g, що індукує абстрактний автомат A другого роду.

8 Приклади автоматів Приклад 4.3. (1) Побудуємо скінченний автомат A‘ першого роду, еквівалентний автомату A другого роду. Підставляючи у зсунуту функцію виходів (q, x) функцію переходів (q, x) (наведені вище) автомата A, одержуємо звичайну функцію виходів (q, x), що визначається таблицею, яку наведено нижче. Функція '(q, x) стосується абстрактного автомата першого роду A' = , що визначає відображення F': Fq1 = {q2(x1/y2), q4(x2/y1), q1(x3/y2)}, Fq2 = {q1(x1/y1), q3(x2/y2), q4(x3/y1)}, Fq3 = {q1(x1/y1), q4(x2/y1), q2(x3/y1)}, Fq4 = {q4(x1/y2), q1(x2/y1), q3(x3/y2)}.

9 Приклади автоматів Приклад 4.3. (2) Графоїд автомата A' подано нижче, а матрицю з'єднань R' – поруч. При подачі на вхід автомата A' вхідних слів p1 і p2 на виході одержимо слова r1 і r2 такі самі, як й у випадку скінченного автомата другого роду A. Тому абстрактний автомат A' інтерпретує абстрактний автомат A.

10 Приклади автоматів Автомати Мура (1) Вихідний сигнал автомата Мура залежить тільки від його стану, тобто y(t)=(q(t)). Тому кожний стан qQ позначено деякою вихідною літерою yY, що ставиться у дужках біля елемента qQ у лівій частині запису відображення F множини Q. Таблиця виходів автомата Мура зводиться, таким чином, до одного рядка, при розміщенні якого над літерами алфавіту станів таблиці переходів приходимо до так званої позначеної таблиці переходів, яка однозначно задає деякий автомат Мура.

11 Приклади автоматів Автомати Мура (2) За геометричної інтерпретації автомата Мура літери вихідного алфавіту yY ставляться у дужках біля відповідних літер qQ алфавіту станів, а у матриці з'єднань записуються над відповідним стовпчиком. Аналітично автомат Мура може бути задано у формі B = , де відображення  будь-якому qQ і кожній літері xX зіставляє стан qkQ, що визначає функцію переходів (q, x), а кожному qQ – вихідну літеру yY, яка визначає зсунуту функцію виходів (q).

12 Приклади автоматів Приклад автомата Мура (1) Приклад 4.4. Нехай задано автомат Мура B = , де X = {x1, x2}, Q = {q1, q2, q3}, Y = {y1, y2}, причому Fq1(y2) = {q2(x1), q3(x2)}, Fq2(y1) = {q3(x1), q2(x2)}, Fq3(y2) = {q1(x1), q2(x2)}. Графоїд автомата показано на наступному слайді. За ним легко записується позначена таблиця переходів, що визначає закон функціонування автомата Мура. Функції (q, x) і (q) наведено у таблиці. Матрицю з'єднань RB автомата B також наведено на наступному слайді.

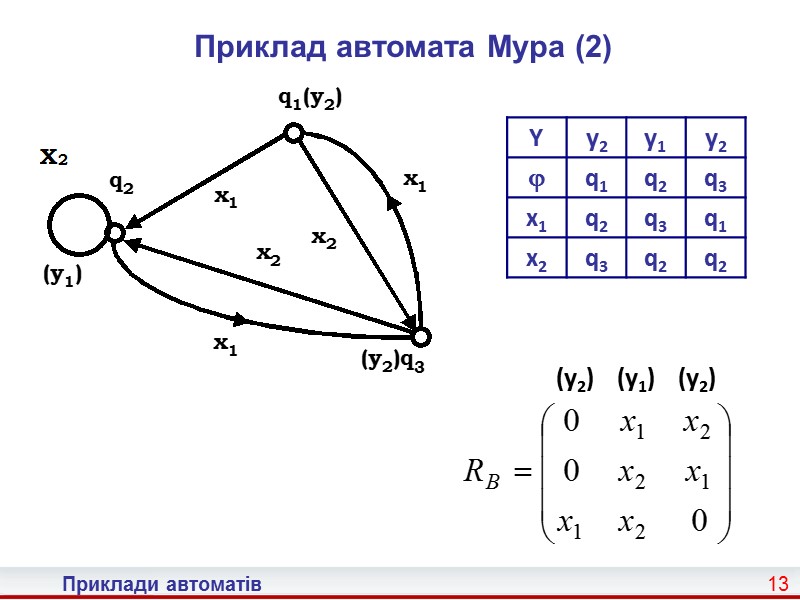
13 Приклади автоматів Приклад автомата Мура (2)

14 Приклади автоматів Інтерпретація автомата Мура автоматом Мілі (1) Приклад 4.5. Побудуємо автомат Мілі A, що інтерпретує автомат Мура B. З використанням позначеної таблиці переходів автомата Мура будуємо звичайну функцію виходів (q, x) (наведено у таблиці нижче), що визначає автомат Мілі А, в якого Fq1 = {q2(x1/y1), q3(x2/y2)}, Fq2 = {q3(x1/y2), q2(x2/y1)}, Fq3 = {q1(x1/y2), q2(x2/y1)}. Геометричну інтерпретацію автомата Мілі A показано на наступному слайді, а матрицю з'єднань наведено поруч. На цьому ж слайді наведено таблицю виходів , а таблиця переходів  співпадає з таблицею у автомата Мура.

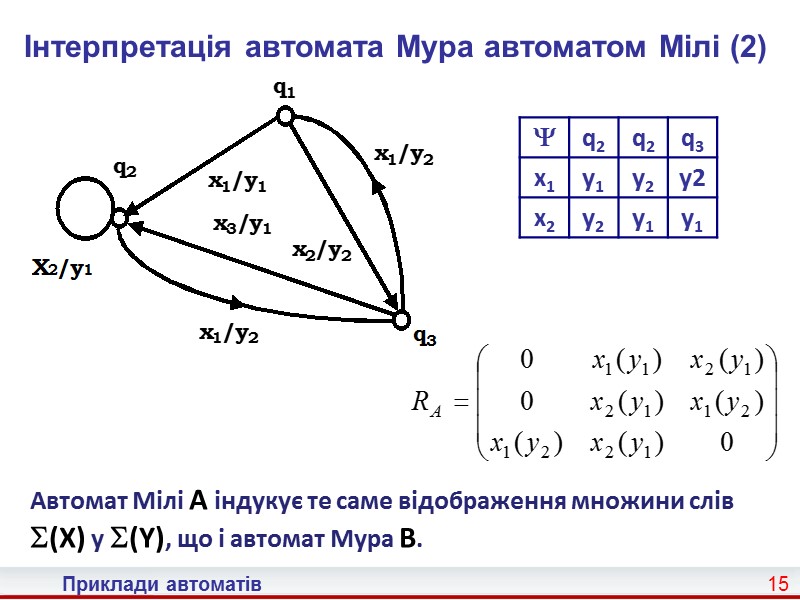
15 Приклади автоматів Інтерпретація автомата Мура автоматом Мілі (2) Автомат Мілі A індукує те саме відображення множини слів (X) у (Y), що і автомат Мура B.

16 Приклади автоматів Часткові автомати Раніше ми розглядали скінченні автомати, в яких відображення  і  визначено для будь-якої пари елементів (q, x)Q  X. Такі автомати називаються цілком визначеними. Автомати, в яких відображення  і  визначено не для всіх пар (q, x)Q  X, називаються частковими автоматами. У тих місцях таблиць переходів і виходів, а також матриць з'єднань автоматів, де відповідні переходи та виходи не визначено, ставитимемо нулі або риски.

17 Приклади автоматів Область заборони автомата Подаватимемо на вхід автомата різноманітні слова вхідного алфавіту. Нехай при подачі вхідної літери хіk деякого слова p = хі1, хі2,…, хіk відповідний їй вихідний сигнал невизначений. У такому випадку кажуть, що вхідне слово p заборонено для даного часткового автомата. Сукупність усіх заборонених слів утворює область заборони автомата. Незаборонені слова називаються припустимими, а їх сукупність – множиною припустимих слів автомата.

18 Приклади автоматів Зв'язний автомат Визначимо поняття зв'язного автомата. Стан qlQ абстрактного автомата називається досяжним, якщо збігається із початковим або існує такий досяжний стан qkQ і така літера вхідного алфавіту xiX, що ql(xi)(qk). У протилежному випадку стан ql називається недосяжним. Абстрактний автомат, усі стани якого є досяжними, називається зв'язним. Автомат не може перейти у недосяжний стан із початкового під впливом припустимих вхідних слів. Тому у матриці з'єднань автомата рядки та стовпчики, позначені недосяжними станами, можна викреслити.

19 Приклади автоматів Ізоморфізм автоматів (1) Два абстрактних автомати A = і B = одного й того самого роду називаються ізоморфними, якщо існують три бієктивні відображення ,  та , відповідно :XZ, :QV, :YU такі, що (q1) = v1. При цьому для будь-яких елементів qQ, xX та yY виконуються співвідношення (q) = ((q), (x)), (y) = ((q), (x)). Треба зауважити, що (x) = z, (q) = v, (y) = u.

20 Приклади автоматів Відношення ізоморфізму між автоматами позначається  та має властивості: A  A (рефлексивність); A  B  B  A (симетричність); (A  B)(B  C)  (A  C) (транзитивність). Тому відношення ізоморфізму на множині скінченних автоматів є відношенням еквівалентності. Ізоморфні автомати за відповідного перепозначення індукують одне й те саме автоматне відображення f. Ізоморфізм автоматів (2)

21 Приклади автоматів