1 НОРМАЛИЗАЦИЯ 2 При проектировании базы данных реляционной

1 НОРМАЛИЗАЦИЯ

2 При проектировании базы данных реляционной СУБД основной целью разработки логической модели данных является создание точного представления данных, связей между ними и требуемых ограничений. Для достижения этой цели необходимо прежде всего определить подходящий набор отношений. Метод, который используется для решения последней задачи, называется нормализацией (normalization).
3 Цель нормализации Нормализация - метод создания набора отношений с заданными свойствами на основе некоторых требований к данным.

4 Избыточность данных и аномалии обновления

5 Функциональные зависимости Функциональная зависимость (functional dependency) описывает связь между атрибутами и является одним из основных понятий нормализации

6 Характеристики функциональных зависимостей Пусть реляционная схема имеет атрибуты (А, В, С, . . Z) Тогда база данных может быть представлена в виде одного универсального отношения R(А, В, С, . . ., Z) Из этого предположения следует, что каждый атрибут в базе данных имеет уникальное имя.

7 Функциональная зависимость Описывает связь между атрибутами отношения. Например, если в отношении содержащем атрибуты А и В, атрибут В функционально зависит от атрибута А (что обозначается как А (В)), то каждое значение атрибута А связано только с одним значением атрибута в. (Причем атрибуты А и В могут состоять из одного или нескольких атрибутов.)

8 Функциональная зависимость Детерминантом функциональной зависимости называется атрибут или группа атрибутов, расположенная на диаграмме функциональной зависимости слева от стрелки.

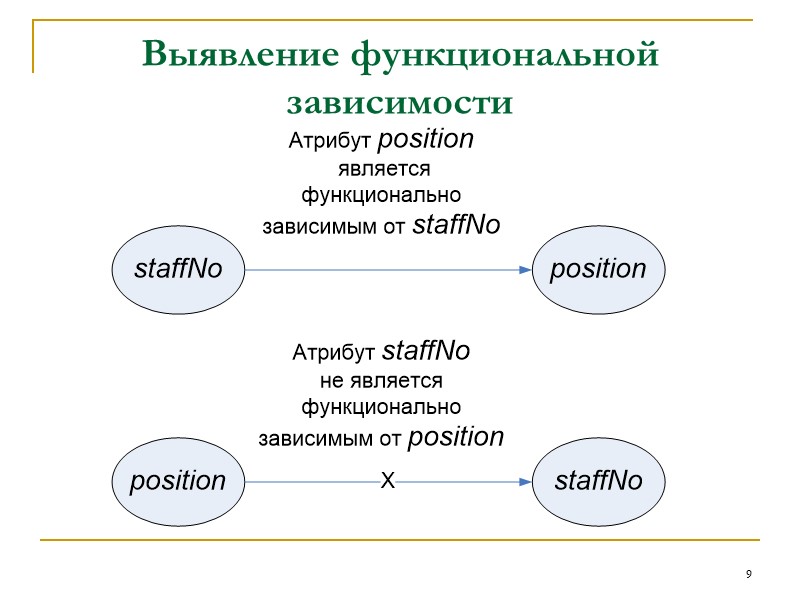
9 Выявление функциональной зависимости

10 Выявление функциональной зависимости, которая остается действительной при всех условиях

11 Тривиальные функциональные зависимости Функциональная зависимость называется тривиальной, если она остается справедливой при любых условиях. К тому же зависимость является тривиальной, если и только если в правой части выражения, определяющего зависимость, приведено подмножество (но необязательно собственное подмножество) множества, которое указано в левой части (детерминанте) выражения.

12 Например:

13 Основные характеристики функциональных зависимостей определяют связь "один к одному" между атрибутами, приведенными в левой и правой частях выражения зависимости; остаются справедливыми при любых условиях; являются нетривиальными

14 Множество всех функциональных зависимостей, которые могут быть выведены из заданного множества функциональных зависимостей X, называется замыканием X и записывается как X*. Для успешной работы необходимо определить ряд правил, позволяющих вычислить X* из X.

15 Правила вывода для функциональных зависимостей Рефлексивность. Если В — подмножество А, то А→В. Дополнение. Если А → В, то А,С → В,С. Транзитивность. Если А → В и В → С, то А → С.

16 Правила вывода для функциональных зависимостей Самоопределение. А → А. Декомпозиция. Если А → В,С, то А → В и А → С. Объединение. Если А → В и А → С, то А → В,С. Композиция. Если А → В и C → D, то А,С → В,D.

17 Минимальное множество функциональных зависимостей Множество функциональных зависимостей Y покрывается множеством функциональных зависимостей X, если каждая функциональная зависимость из Y присутствует также в замыкании X*. Иными словами, каждая функциональная зависимость во множестве Y может быть выведена из X.

18 Минимальное множество функциональных зависимостей Множество функциональных зависимостей X является минимальным, если оно удовлетворяет следующим условиям: Каждая зависимость в X имеет единственный атрибут в правой части. Ни одну зависимость А → В в X нельзя заменить зависимостью С → В, где С является собственным подмножеством А, и получить в результате множество зависимостей, эквивалентное X. Из множества X нельзя удалить ни одной зависимости и получить в результате множество зависимостей, эквивалентное X.

19 Процесс нормализации Нормализация — это формальный метод анализа отношений на основе их первичного ключа (или потенциальных ключей) и существующих функциональных зависимостей

20 Реляционные ключи Суперключ (superkey) Атрибут или множество атрибутов, которое единственным образом идентифицирует кортеж данного отношения. Потенциальный ключ. Суперключ, который не содержит подмножества, также являющегося суперключом данного отношения

21 Реляционные ключи Первичный ключ. Потенциальный ключ который выбран для уникальной идентификации кортежей внутри отношения. Внешний ключ. Атрибут или множество атрибутов внутри отношения, которое соответствует потенциальному ключу некоторого (может быть, того же самого) отношения.

22 Таблица, содержащая одну или несколько повторяющихся групп данных. Ненормализованная форма (ННФ).

23 Последовательность нормальных форм: первая нормальная форма (1NF); вторая нормальная форма (2NF); третья нормальная форма (3NF); нормальная форма Бойса-Кодда (BCNF); четвертая нормальная форма (4NF); пятая нормальная форма, или нормальная форма проекции-соединения (5NF или PJ/NF).

24 Основные свойства нормальных форм: каждая следующая нормальная форма в некотором смысле лучше предыдущей; при переходе к следующей нормальной форме свойства предыдущих нормальных свойств сохраняются.

25 Первая нормальная форма (1НФ). Отношение, в котором на пересечении каждой строки и каждого столбца содержится одно и только одно значение (значения всех атрибутов отношения атомарны ).

26 Первая нормальная форма (1НФ). Для преобразования ненормализованной таблицы в первую нормальную форму (1НФ) в исходной таблице следует найти и устранить все повторяющиеся группы данных. Повторяющейся группой называется группа, состоящая из одного или нескольких атрибутов таблицы, в которой возможно наличие нескольких значений для единственного значения ключевого атрибута (атрибутов) таблицы.

27 Способы исключения повторяющихся групп: Повторяющиеся группы устраняются путем ввода соответствующих данных в пустые столбцы строк с повторяющимися данными. (Пустые места при этом заполняются дубликатами неповторяющихся данных.)

28 Способы исключения повторяющихся групп: Атрибут или группа атрибутов назначаются ключом ненормализованной таблицы, а затем повторяющиеся группы изымаются и помещаются в отдельные отношения вместе с копиями ключа исходной таблицы. Далее в новых отношениях устанавливаются свои первичные ключи.

29 Вторая нормальная форма (2НФ) Полная функциональная зависимость. Если А и В - атрибуты отношения, то атрибут В находится в полной функциональной зависимости от атрибута А, если атрибут В является функционально зависимым от А, но не зависит ни от одного собственного подмножества атрибута А.
30 Вторая нормальная форма (2НФ) Функциональная зависимость А → В является полной функциональной зависимостью, если удаление какого-либо атрибута из А приводит к утрате этой зависимости. Функциональная зависимость А → В называется частичной, если в А есть некий атрибут, при удалении которого эта зависимость сохраняется.

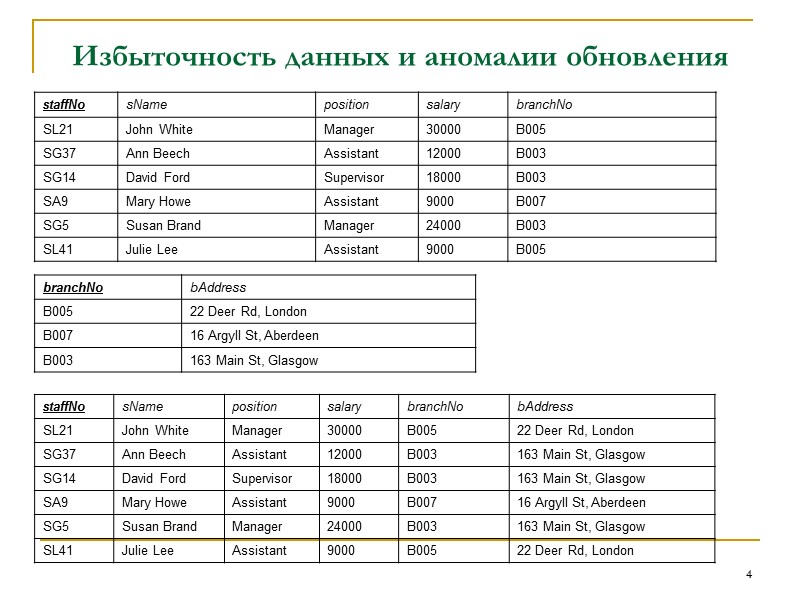
31 Например функциональная зависимость: staffNo, sName → branchNo Здесь каждая пара значений (staffNo, sName) связана с единственным значением branchNo. Однако эта функциональная зависимость не является полной, поскольку branchNo также функционально зависит от подмножества (staffNo, sName), т.е. от атрибута staffNo.

32 Вторая нормальная форма (2НФ). Отношение, которое находится в первой нормальной форме и каждый атрибут которого, не входящий в состав первичного ключа, характеризуется полной функциональной зависимостью от этого первичного ключа.

33 Третья нормальная форма (ЗНФ) Транзитивная зависимость. Если для атрибутов А, В и С некоторого отношения существуют зависимости вида А → В и → С, это означает, что атрибут С транзитивно зависит от атрибута А через атрибут В (при условии, что атрибут А функционально не зависит ни от атрибута В, ни от атрибута С).

34 Третья нормальная форма (ЗНФ) Определение Отношение, которое находится а первой и во второй нормальных формах и не имеет атрибутов, не входящих в первичный ключ атрибутов, которые находились бы в транзитивной функциональной зависимости от этого первичного ключа.
35 Общее определение второй и третьей нормальных форм Вторая нормальная форма (2НФ). Отношение, находящееся в первой нормальной форме, в котором каждый атрибут, отличный от атрибута первичного ключа, является полностью функционально независимым от любого потенциального ключа.
60-lekciya_6.ppt
- Количество слайдов: 37
