1 ЛОГІКИ КВАЗІАРНИХ ПРЕДИКАТІВ 1 -го ПОРЯДКУ

1 ЛОГІКИ КВАЗІАРНИХ ПРЕДИКАТІВ 1 -го ПОРЯДКУ Розглядаємо композиційно — номінативні логіки еквітонних квазіарних предикатів – неокласичн і логік и Чиста неокласична логіка ЧНКЛ – це НКЛ еквітонних предикатів кванторного рівня Семантичні моделі ЧНКЛ – композиційні системи еквітонних квазіарних предикатів кванторного рівня ( V A , P r A , C ), де C визначається множиною базових композицій Кожна така КС задає АС даних ( A , Е P r A ) та композиційну алгебру предикатів кванторного рівня. ( P r А , C ) Побудова композиційні алгебри предикатів кванторного рівня визначає мову ЧНКЛ. А лфавіт мови: – V – множина предметних імен – Ps –множина предикатнихсимволiв (ПС) – імен базових предикатів – символи базових композицій Множину Ps назвемо сигнaтурою мови ЧНКЛ. { , , R , }. v xx , , , v x. R x

21. Кожний ПС є формулою. Такi формули назвемо атомарними. 2. Нехай – формула. Тодi – формули. 3. Нехай та – формули. Тодi – формула. Множину всіх формул позначимо Fr. Як і для мов ПЛ та РНЛ, використовуємо скорочення формул. ( ) – множина всіх тих р Рs , які входять до складу формули . nm ( ) – множина всіх предметних імен v V, які фігурують в символах реномінації формули . Така nm ( ) – множинаімен формули . q ( ) – множина всіх v V, які фігурують в символах квантифікації, що входять до складу . Така q ( ) – множинакванторнихімен формули . nq ( ) = nm ( ) \ q ( ) – множинанекванторнихімен формули . Розширюємо , пт , q , nq на множини формул , , v x. R x

3Інтерпретуємо мову ЧНКЛ на КС еквітонних предикатів кванторного рівня. Задамо тотальне однозначне I : Ps Е P r A , яке визначає значення ПС як базові предикати відповідної АС даних ( А , Е P r A ) Такі АС даних – неокласичн i АСізеквітоннимипредикатами. Відображення I прив’язує АС даних ( А , Е Pr A ) до мови. Отримуємо об ‘ єкти вигляду (( A , ЕPr A ), I ) – АСЕПздоданоюсигнатурою. Така АС фактично визначає KC ( V A , Е P r A , C ) АС з доданою сигнатурою (( A , ЕPr A ), I ) позначаємо ( A , I ). АС з доданою сигнатурою є інтегрованими семантичними моделями, які пов’язують мову ЧНКЛ із АС даних. Називаємо їх моделямимови Для інтерпретації формул продовжимо I до відображення Fr Е P r

41. I ( ) = ( I ( )). 2. I ( ) = ( I ( ), I ( )). 3. 4. I ( x ) = x ( I ( )). Предикат I ( ) – значення формули при інтерпретації A =( A , I ) Позначаємо його A (частково) істинна, або неспростовна при інтерпретації A = ( A , I ), або A — істинна, якщо A – істинний предикат. Цей факт позначимо A |= . виконуванаприінтерпретації A =( A , I ), або A -виконувана , якщо A – виконуваний предикат. всюдиiстинна, якщо iстинна при кожнiй iнтерпретацiї. Цей факт позначимо |= . виконувана, якщо виконувана при деякiй iнтерпретацiї. ( ) R ( ( ))v v x x. I R I

5 Успадкування властивостей ПЛ для ЧНКЛ відбувається перенесенням на рівень ЧНКЛ понять тавтології, тавтологічних наслідку і еквiвалентностi. Тавтологiї – формули, якi мають структуру тавтологiй мови ПЛ. Формула пропозиційнонерозкладна, якщо вона атомарна або вигляду чи x F r 0 – множина всiх пропозиційно нерозкладних формул мови L. Iстиннiснаоцiнка мови L– довiльне : F r 0 { T , F }. Продовжимо до вiдображення : F r { T , F }: – ( )= T ( )= F ; – ( )= T ( )= T або ( )= T. тавтологiя , якщо ( )= T при кожнiй iстиннiснiй оцiнцi Кожнатавтологіяєвсюдиістинноюформулою. Приклад. Формули вигляду x y y x всюди iстинні, але не тавтологiї. v x. R

6 На множинi формул мови ЧНКЛ введемо відношення тавтологiчного наслiдку ╞ , тавтологiчної еквiвалентностi т , логiчного наслiдку |=, слабкого логiчного наслiдку ||= логiчної еквiвалентностi . є тавтологiчним наслiдком ( позн. ╞ ) , якщо – тавтологiя. та тавтологiчноеквiвалентнi ( позн. т ): ╞ та ╞ є логiчнимнаслiдком ( позн. |= ): всюди iстинна. та логiчноеквiвалентнi ( позн. ): |= та |= . Зрозумiло, що формули та всюди iстиннi. є слабкимлогiчнимнаслiдком формули , що позн. ||= , якщо A iз A |= випливає A |= .

7 Основнівластивостівідношень ╞, |=, ||= та : 1) тавтологія ╞ ; 2) всюди істинна |= ||= ; 3) ╞ |= ; але не завжди |= ╞ ; 4) |= ||= ; але не завжди ||= |= ; 5) т тавтологія 6) |= ; 7) відношення ╞ , |= та ||= рефлексивні і транзитивні; 8) відношення рефлексивне, транзитивне і симетричне.

8 Теорема 1 (про розширення). Нехай. АСоднієїсигнатури A = ( А , IА ) і В = ( А , IВ ) таформула такі: р ( ) V Aізр. A ( ) випливаєр. В ( ) = р. A ( ). Тоді d V A із A ( d ) випливає В ( d ) = A ( d ). Доводиться індукцією за побудовою формули . Т еорема вірна для загального випадку логік квазіарних предикатів. Нехай A = ( А , IА ) і В = ( А , IВ ) – АС одн i є ї сигнатури. АС В – систем а розширень для АС A , якщо р Ps V A із р A ( ) випливає р. В ( ) = р. A ( ). Наслідок. Нехай В = ( А , IВ ) – системарозширеньдля АС A = ( А , IА ). Тодідлядовільних та d V A із A ( d ) випливає В ( d ) = A ( d ).

9Ім’я x V неiстотнедляформули , якщо A = ( A , I ) x неiстотне для A. Критерій неістотності предметних імен для формул встановлює Теорема 2. Ім’я x V неістотнедля |= x Враховуючи , що завжди |= x та |= x , дістаємо Наслідок. Ім’яx V неістотнедля |= x Неістотні імена дають змогу робити перейменування квант. імен. Теорема 3. Нехайу V неістотнедля . Тоді Наслідок. Нехай у V неістотнедля . Тоді Основою евівалентних перетворень формул ЧНКЛ є Теорема 4 (семантичної еквiвалентостi). Нехай ‘ отриманаiз замiноюдеякихвходженьформул 1 , . . . , n на 1 , . . . , n вiдповiдно. Якщо 1 1 , . . . , n n , то ‘| ( )x yx R | ( )x yx y. R

10 Семантичні властивості ЧНКЛ Для ЧНКЛ успадковуються властивості пропозиційного рівня. Із реномінативного рівня успадковуємо специфічні властивості формул, пов ‘ язані з реномінацією. RT) Згортка тотожної пари імен у реномінації: R ) R -дистрибутивність: Аналогічно – властивості R , R&, R . RR) Згортка реномінацій: R N ) Нехай у неістотне для формули . Тоді , , | ( ) z v v z x x R R | ( )v v x x. R R | ( ) ( )v v v x x x. R R R | ( ( )) ( )v w x y x y. R R R o , , | ( )y v v z x x. R R

11 Вкажемо властивості кванторного рівня, які не використовують реномінації. Вони цілком аналогічні властивостям класичної логіки: S 1) x та x S 2) x . S 3) x та x , але не завжди x . S 4) Якщо , то x , x та x . S 5) Якщо , то x x та x x . S 6) Якщо та x , то x . S 7) Якщо та x , то x . S 8) x y y x та x y y x . S 9) x x x ; x x x . S 10) y x x y , але не завжди x y y x S 11) x x та x x . S 12) x x . S 13) x x x ( ) та x & x x ( & ). S 14) x ( & ) x & x та x x x ( ).

12 Властивості, пов ‘ язані з композиціями квантифікації та реномінації : R х ) х R) N R) при х { у , u 1 , . . . , u n } аналітична неістотність верхніх імен в реномінаціях Зокрема, при х у маємо R ) при обмежена R — дистр — ть RZ) Нехай х неістотне для . Тоді у V маємо : згортка за неістотн им імен ем. Зокрема, RВ) Зокрема, 1 1 , . . . , 1, . . . , | ( ). . . n n v v nx x. R v v 1 1 , . . . , 1, . . . , |. . . ( )n n v v nx xv v R 1 1 , , . . . , | ( )n n х v v у u ux. R R | ( )х х у уx. R R | ( )v v u u. R x x. R { , }x v u 1 1 , , . . . , | ( )n n х v v у u u. R R | ( )х у. R 1 1 , , . . . , | ( ) ( ))n n х v v у u ux R R | ( ) ( ( ) ))х уx R

13 Умова є істотною для властивості R . Справді: при v u ; Для пронесення символів реномінації через х , якщо умова для R не виконується, потрібно спочатку замінити підформулу х на де z неістотне для та z { v 1 , . . . , v n , u 1 , . . . , u n }. Тому для виконання еквівалентних перетворень довільних формул треба мати потенційно нескінченний запас неістотних імен. Це дає змогу пронести символи реномінації вглиб формули і перетворити формулу до вигляду, близького до класичного, коли реномінації застосовні тільки до ПС. Для формул класичної логіки істотними є тільки їх вільні предметні імена, від яких можезалежати значення відповідних предикатів. В класичній логіці базового предикату за допомогою спеціальної функціїарності ar : Ps N визначається скінченна стандартна множина істотних імен: для п -арного предикату істотними є саме імена 1, …, п. Для НКЛ важлива в першу чергу неістотність предметних імен. Тому для базових предикатів НКЛ будемо вказуємо множину неістотних імен, від яких незалежить значення таких предикатів. { , }x v u | ( )v v u uv. R R | ( ) та | ( )v v v uv. R v v | ( )v v u uu. R R u ( ), х zz. R

14Імена, неістотність яких для базових предикатів постулюється, називаються синтетичнонеістотними. Нехай для визначення синтетично неістотних імен задана : Ps 2 V. Таку функцію продовжимо до : Fr 2 V : ( ) = ( ); = ( ( ) { v 1 , . . . , v n }) \{ x i | v i ( ), i {1, …, n }. ( x ) = ( ) { x } Пару ( Ps , ) назвемо сигнатуроюсинтетичноїнеістотності. Така сигнатура є аналогом сигнатури класичної логіки ( Ps , ar ). На відміну від класичного випадку, вона не впливає на множину формул НКЛ, але обмежує клас інтерпретацій. Тотальна неістотність імені x означає Тому при завданні синтетично неістотних імен за допомогою функції множиною тотально неістотних імен буде Постулювання наявності нескінченної множини тотально неістотних імен вима гає, щоб V T була нескінченною. 1 1 , . . . , ( )n n v v x x. R ( ) p Ps x p I ( )T p Ps V p I

15 Отже, для НКЛ розглядаємо тільки такі мови та інтерпретації, для яких задана функція , що гарантує нескінченність Теорема 5. Нехайх ( ). Тодіхнеістотнедля Наслідок. Якщо x ( ), то |= x та |= x Якщо для умова не виконується, то візьмемо тотально неістотне z : O тримуємо загальну R — дистрибутивність: R ) тут z тотально неістотне та ( )T p Ps V p I ( )v u. R x ( ( ))v uz nm R x ( )v v x u u z. R x z. R o ( ( ))v uz nm R x { , }x v u

16 Нормальні форми в ЧНКЛ Ψ – варіанта формули Ξ, якщо Ψ утворена із Ξ посл. замінами підформул вигляду х на підформули при умові у ( ). Теорема (про варіанту). Нехай Ψ – варіантаформули Ξ. Тоді |= Ψ Ξ. Формула Ψ – в різнокванторній формі, якщо всі входження кванторних префіксів у формулу Ψ (якщо вони є) по різних тотально неістотних іменах, причому кожне у q (Ψ) не може лежати в області дії такого, що Формулу в різнокванторній формі назвемо різнокванторною. Формула Ψ – в нормальнійформі , якщо всі символи реномінації формули Ψ (якщо вони є) застосовані тільки до ПС, та всі входження кванторних префіксів у Ψ – по різних тотально неістотних іменах. Отже, Ψ – в нормальній формі, якщо вона різнокванторна та всі символи реномінації формули Ψ (якщо вони є) застосовані тільки до ПС. Формулу в нормальній формі назвемо нормальною. ( )х yy. R v x. R { , }y v x

17 Теорема. Длякожної можназбудуватирізнокванторну : |= Ξ Кожному входженню х в зі ставимо нове тотально неістотне ім’я із V , причому різним входженням кванторних префіксів зі ставимо різні тотально неістотні імена. Просуваючись по зліва направо, замінюємо кожну підформулу вигляду х А на формулу де у – тотально неістотне і м’я, співставлене такому входженню х в . Так збудована різнокванторна, в силу маємо |= . Зрозуміло, що – варіанта формули Теорема. Длякожної можназбудуватинормальну Ψ: |= За побудуємо її варіанту – різнокванторну 1. Тоді |= 1 За 1 будуємо Ψ. Використовуючи R , RR, проносимо всі символи реномінації вглиб формули до рівня ПС. Отримуємо Ψ таку, що |= 1 . При цьому всі входження кванторних префіксів в Ψ – по різних тотально неістотних іменах. Отже, Ψ – нормальна, а в силу |= 1 та |= 1 маємо |= Нормальну формулу Ψ, отриману із даної формули так описаним способом, назвемо нормалізантою формули Наслідок. Нехай Ψ нормалізантаформули . Тоді |= ( ), х yy. R A | ( )х yx. A y. R

18 Визначимо множину fr ( ) квазівільни х імен формули . Для цього задамо функцію fr : Fr 2 V : р Ps покладемо fr ( р ) = . Далі значення fr визначаємо індуктивно: fr ( ) = fr ( ); fr ( x ) = fr ( ) \{ x }; ( fr ( )\{ v 1 , . . . , v n }) { x 1 , . . . , x n }. Звідси fr ( x ) = fr ( x ) = fr ( ) \{ x } та Для встановлення неістотності предметних імен важливою є Теорема. Якщо у ( р ) ПС рф-ли та у fr ( ), то у ( ). Теорема доводиться індукцією за побудовою формули . Наслідок 1. Нехай у Vнеістотне ПСформули та у nm ( ). Тоді у ( ). В силу fr ( ) пт ( ) з умови у пт ( ) випливає умова у fr ( ). Наслідок 2. Нехай у Vтотальнонеістотне та у nm ( ). Тодіу ( ). Формула квазізамкнена , якщо fr ( )= . 1 1 , . . . , ( )n n v v x xfr R ( ( )) ( ) \ { }х yfr y. R fr x

19 Квазізамкнені формули є синтаксичними аналогами замкнених формул класичної логіки, проте семантичними аналогами замкнених формул їх вважати не можна. До складу формули можуть входити ПС, для яких множини істотних імен нескінченні. Можливість для формули бути залежною від нескінченної множини предметних імен є визначальною властивістю логіки квазіарних предикатів, зокрема, НКЛ, що істотно її відрізняє від класичної логіки. Пропозиційною схемою формули назвемо ПФ Prop ( ), отриману із опусканням усіх символів, окрім ПС та символів проп. зв ‘ язок. Теорема. Нехай формул a квазізамкнена, Prop ( ) не тавтологія і не суперечність, причому не містить спеціальних ПС із явно виділенимиістотнимиіменами ( наприклад, символирівності = ху ). Тоді існують. АС A = ( А , I ) та d 1 , d 1 V A такі, що А ( d 1 ) = T та А ( d 2 ) = F. Якщо Prop ( ) не тавтологія і не суперечність, то існують істиннісні оцінки 1 , 2 такі, що 1 ( Prop ( )) = T та 2 ( Prop ( )) = F. Візьмемо z V : z nm ( ) та z ( ). Візьмемо А = { a , b }. d A nm ( ) та р ( ) визначимо р А ( d ) . d A nm ( ) та р ( ) задамо р А ( d z a ) = 1 ( p ) та р А ( d z b ) = 2 ( p ). Тоді А ( d z a ) = T та А ( d z b ) =

20 Таким чином, для логіки квазіарних предикатів квазізамкнені формули необов ‘ язково інтерпретуються як константні предикати. У той же час для випадку класичної логіки кожна замкнена формула на кожній АС відповідної сигнатури завжди інтерпретується як як T або F Теорема. формули можнапобудуватиквазізамкненун ормальну формулу таку, що |= . За спочатку будуємо її різнокванторну варіанту 1 Якщо fr ( ) = fr ( 1 ) = , далі будуємо нормальну формулу Ψ Позаяк fr (Ψ) = fr ( 1 ) = , то Ψ квазізамкнена, вона нормалізант a формули , тому |= . Звідси |= , тому – шукана формула . Нехай fr ( ) = fr ( 1 ) = { u 1 , . . . , u k }≠ . Візьмемо множину { у 1 , . . . , у k } тотально неістотних імен таких, що { у 1 , . . . , у k } nm ( 1 )= . Всі у 1 , . . . , у k неістотні для 1. Т оді |= 1 |= u 1 … u k 1 , звідки |= u 1 … u k 1 2 , де 2 – це формула . З від с и |= 1 |= 2 . Згідно R , RR проносимо всі реномінації вглиб формули до рівня ПС. Отримуємо таку, що |= 2 . При цьому fr ( )= , всі входження кванторних префіксів в – по різних тотально неістотних іменах. Отже, квазі замкнена – в нормальній формі, згідно |= 1 , |= 1 2 та |= 2 маємо |= . Така – квазізамкненанормалізанта формули . 1 1 , . . . , 1 1, . . . k k u u ky yy y R

21 Відношення логічного наслідку для множин формул ЧНКЛ та – множини формул мови сигнатури Ps. A = ( А , I ) – АС сигнатури Ps. є логічнимнаслідком в АС A , якщо d V A А ( d )= T неможливо Ψ А ( d )= F Ψ . Позначаємо |= А є логічнимнаслідком , якщо |= А АС A = ( А , I ) сигнатури Ps. Це позначаємо |= Звідси: | існують АС A = ( А , I ) та d V A такі: маємо А ( d )= T та Ψ маємо Ψ А ( d )= F Відношення |= для множин формул рефлексивне, але не транзитивне Теорема ( заміниеквівалентних ). Нехай . Тоді , |= та |= , .

22 В ластивості в ідношення |= G 1, G 2 та П 1–П 10 успадковуються на кванторному рівні Вкажемо властивості відношення |= , пов‘язані з композиціями реномінації та квантифікації. Вони безпосередньо відтворюють відповідні властивості формул. Кожна така властивість розщеплюється на дві властивості для |= RT ) RT ) RR ) , , ( ), | z v v z x x. R R , , | , ( ) z v v z x x. R R ( ( )), | ( ), |v w x y x y. R R R o | , ( ( )) | , ( )v w x y x y. R R R o ( ), |v v x x. R R

23 R ) Ps. N ) при у ( р ), де р Ps N ) при умов і у ( ). N ) при умові у ( ). Умову у ( ) можна ослабити до умови унеістотнедля . Базовівластивості відношення |= на реномінативному рівні: П 1–П 4 та RT |- , RТ-| , RR|- , RR-| , R |- , R -| , Ps. N|- , Ps. N-| ( ), |v v v x x x. R R R | , ( ) | , ( )v v v x x x. R R R , , ( ), |y v v z x x. R p , , | , ( ) y v v z x x R p , , ( ), |y v v z x x. R R , , | , ( ) y v v z x x. R R

24 Властивості, пов‘язані з кванторами та реномінаціями: R ) Для R та R z тотально неістотне та Вл-ті R , R переформульовуються для х. ( ), | при умові { , }v v x x. R y y. R y v x | , ( ) при умові { , }v v x x. R y y. R y v x ( ), | при умові { , }v v y x x z. R y v x o | , ( ) при умові { , }v v y x x z. R y z R y v x o ( ( )v xz nm R y

25 Властивості, пов‘язані з елімінацією кванторів: ) ) ) Базовівластивості відношення |= на кванторному рівні: П 1–П 4 та RT |- , RТ-| , RR|- , RR-| , R |- , R -| , Ps. N|- , Ps. N-| , N , N- , R , , , | ( ), | при умові та ( , , )x y Tx R y V y nm 1| , ( ), . . . , ( ), | , n x x y y. R R x x 1( ), . . . , ( ), , |n x x y y. R R x x | , ( ) при умові та ( , , )x y Tx R y V y nm

26 C емантично несуперечливі множини формул Множина формул семантичнонесуперечлива ( сумісна ), якщо існують АС A = ( А , I ) та d V A такі, що А ( d )= T для всіх . Звідси: семантичносуперечлива ( несумісна ), якщо неіснують АС A = ( А , I ) та d V A такі, що А ( d )= T для всіх . Модельсумісності множини формул – це АС A =( A , I ) така : для деякого d V A маємо А ( d )= T . Теорема 1. сем. несуперечлива маємодельсумісності. Теорема 2. сем. несуперечлива маємо | & Наслідок. сем. суперечлива длядеякої маємо |= & Теорема 3. Якщо сем. суперечлива , то маємо |= . Якщо | для деякої , то існують АС A = ( А , I ) та d V A : А ( d )= F та А ( d )= T . Але А ( d )= T означає несуперечливість Модель істинності множини формул – це АС A =( A , I ) така: d V A маємо А ( d ) T. Для логік ПЕП кожна модель істинності є моделлю сумісності. Для логік ЕП це невірно: розгл. АС, де ПС інтерпретується як усюди невизначений пр-т Кожна АС із ЕП може бути довизначена до АС із ПЕП.

27 Неокласичні логіки функціонально-екваційного рівня ФЕНКЛ – це НКЛ функціонально-екваційного рівня – ФКНЛР ЕП Семантичні моделі ФЕНКЛ – КС еквітонних квазіарних функцій і предикатів функціонально-екваційного рівня ( V A , ЕFn A ЕPr А , C ) C визначається множиною базових композицій ( ЕFn A ЕPr А , C ) – композиційна алгебра квазіарних функцій і предикатів функціонально-екваційного рівня. Побудова такої алгебри визначає мову ФЕНКЛ. А лфавіт мови ФЕНКЛ – V – множина предметних імен – Fn s – множина функціональних (ФНС) символiв – Dns – множина деномінаційних (ДНС) символiв – Ps – множина предикатних (ПС) символiв – символи базових композицій Множину Fп s Dns позначимо F s. Множину Fn s Ps назвемо сигнaтурою мови ФЕНКЛ. { , , , S , , }. vx ‘x , , . vx S

28 Множини термів Тr і формул Fr вводимо індуктивно. Т 1. Кожний ФС є термом. Такi терми назвемо атомарними. Т 2. Нехай , t 1 , . . . , t n – терми. Тодi – терм. Ф 1. Кожний ПС є формулою. Такi формули назвемо атомарними. Ф 2. Нехай t та s – терми. Тодi = ts – формул a. Ф 3. Нехай – формул a, t 1 , . . . , t n – терми. Тодi – формул a Ф 4. Нехай та – формули. Тодi , та x – формули. ( ) – множина сигнатурних символів терм a чи формули . nm ( ) – множина всіх v V, які фігурують в символах суперпозиції та квантифікації формули . Така nm ( ) – множинаявнихімен формули . d nm ( ) – множина всіх v V, відповідних до ДНС формули . n d n ( ) = nm ( ) d nm ( ) – множинаімен формули . q ( ) – множина всіх v V, які є в символах квантифікації ф-ли . nq ( ) = n d n ( ) \ q ( ) Розширюємо , пт , d nm , n d n , q , nq на множини формул 1, . . . , 1. . . nv v n. S t t

29 Множина fr ( ) квазівільних імен формули : f Fns р Ps покладемо fr ( f ) = fr ( р ) = . ДНС ‘ х покладемо fr ( ‘x ) = { x }. fr ( = ts ) = fr ( t ) fr ( s ); fr ( ) = fr ( ); fr ( ) = fr ( ); fr ( x ) = fr ( ) \{ x }; 1 , . . . , 1 1 1(. . . ) ( ( ) \ { , . . . , }) ( ) n n v v n n i ifr S t t fr v v fr t U U

30Інтерпретуємо мову ФЕНКЛ на КС еквітонних квазіарних ф-ій та пр-ів Задамо тотальне однозначне I : F s Р s ЕFn. A ЕP r. A , яке визначає значення сигнатурних символів ПС як базові функції та предикати відповідної АС даних ( А , ЕFn A ЕP r. A ) При цьому I ( ’v ) = ’v ’v Dns. Такі АС даних – неокласичн i АС із еквітонними функціями та предикатами. Отримуємо об ‘ єкти (( A , E Fn A E P r. A ), I ) – АС ЕФ та ЕП з доданою сигнатурою. Кожна така АС фактично визначає KC ( V A , E Fn. A E P r. A , C ) АС з доданою сигнатурою (( A , E Fn A E P r. A ), I ) скорочено позначаємо ( A , I ). АС з доданою сигнатурою є інтегрованими семантичними моделями, які пов’язують мову ЧНКЛ із АС даних. Називаємо їх моделямимови Продовжимо I до відображення Fr Тr ЕFn A ЕРr. А : 2. I ( = ts ) = = ( I ( t ) , I ( s ) ). 4. I ( ) = ( I ( )). 5. I ( ) = ( I ( , I ( )). 6. I ( x ) = x ( I ( )). 1 1, . . . , 1 11. (. . . ) S ( ( ), . . . , ( ))n nv v n n. I S t t I I t 1 1, . . . , 1 13. (. . . ) S ( ( ), . . . , ( ))n nv v n n. I S t t I I t

31 Функцію I ( t ) – значення терма t при інтерпретації A =( A , I ), – позн. t A. Предикат I ( ) – значення формули при інт-ї A =( A , I ), – позн. A. Поняття істинності та виконуваності формул – аналог. випадку ЧНКЛ. Поняття тавтології, тавт. наслідку, тавт. еквiвалентностi для ФЕНКЛ успадковуються з реномінаційного та кванторного рівнів. Формула пропозиційнонерозкладна , якщо вона атомарна або має вигляд = ts , x чи Визначення та властивості відношень логiчного наслiдку, слабкого логiчного наслiдку та логiчної еквiвалентностi для ФЕНКЛ аналогічні відп. визначенням та властивостям для класичної логіки, РНЛ та ЧНКЛ. Семантичні власт-ті формул ФЕНКЛ індуковані відп. вл-ми композицій. Для пропозиційних композицій та кванторів такі властивості аналогічні відповідним властивостям формул класичної логіки. Розглянемо властивості, пов ‘ язані з композиціями – квантифікації – суперпозиції – рівності 1, . . . , 1. . . nv v n. S t t

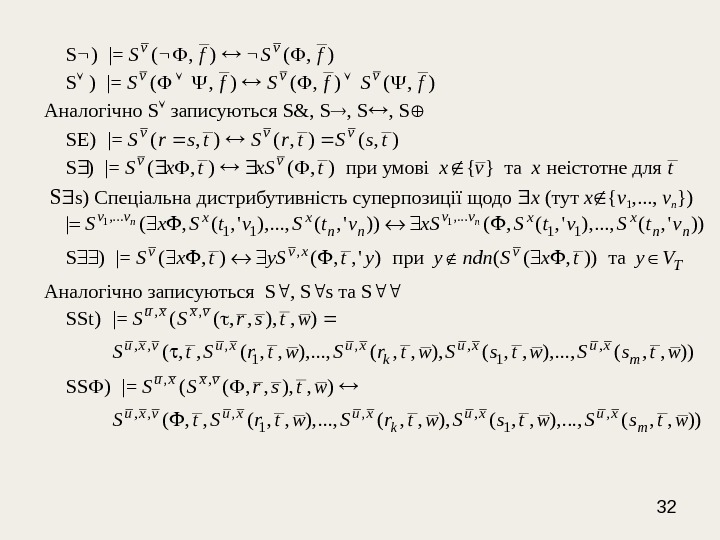32 Аналогічно S записуються S& , S , S S s ) Спеціальна дистрибутивність суперпозиції щодо x (тут х { v 1 , . . . , v n }) Аналогічно записуються S , S s та S S ) |= ( , ) v v S f S ) |= ( , ) v v v S f S f SE) |= ( , ) v v v S r s t S r t S s t S ) |= ( , ) при умові { } та неіст отне для v v S x t x. S t x v x t 1 1, . . . 1 1 1 1| ( , ( , ‘ ), . . . , ( , ‘ ))n nv v v vx x n n n n. S x S t v x. S S t v , , SSt) |= ( ( , , ) u x x v S S r s t w , , , 1 1( , , ), . . . , ( , , ))u x v u x u x k m. S t S r t w S s t w , , SS ) |= ( ( , , )u x x v S S r s t w , , , 1 1( , , ), . . . , ( , , ))u x v u x u x k m. S t S r t w S s t w , S ) |= ( , ) ( , , ‘ ) при ( ( , )) та v v x v TS x t y. S t y y ndn S x t y V

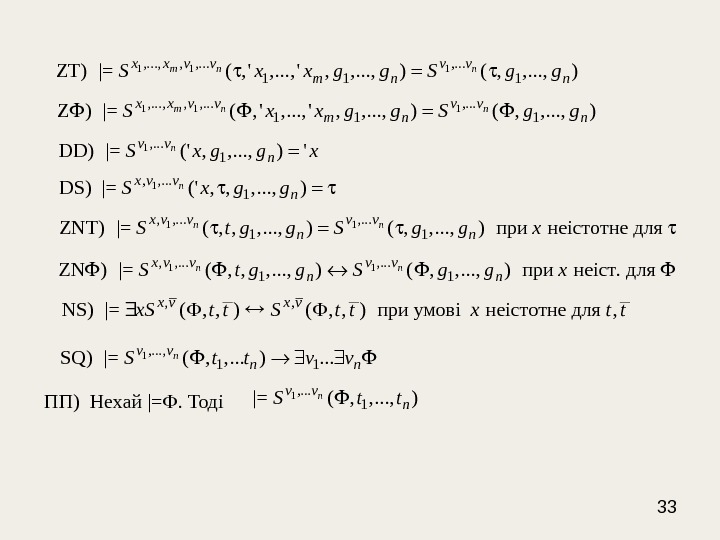33 ПП) Нехай |= . Тоді 1 1 1, . . . , , , . . . 1 1 1 ZT) |= ( , ‘ , . . . , ‘ , , . . . , ) ( , , . . . , )m n nx x v v m n n. S x x g g S g g 1 1 1, . . . , , , . . . 1 1 1 Z ) |= ( , ‘ , . . . , ‘ , , . . . , ) ( , , . . . , )m n nx x v v m n n. S x x g g S g g 1, . . . 1 DD) |= (‘ , , . . . , ) ‘nv v n. S x g g x 1, , . . . 1 DS) |= (‘ , , , . . . , )nx v v n. S x g g 1 1, , . . . 1 1 ZNT) |= ( , , , . . . , ) ( , , . . . , ) при неістотне для n nx v v n n. S t g g S g g x 1 1, , . . . 1 1 ZN ) |= ( , , , . . . , ) ( , , . . . , ) при неіст. для n nx v v n n. S t g g S g g x , , NS) |= ( , , ) при умові неістотне для , x v x. S t t x t t 1, . . . , 1 1 SQ) |= ( , , . . . ). . . nv v n n. S t t v v 1, . . . 1|= ( , , . . . , )nv v n. S t t

34 С пецифічнівластивостірівності. Rf ) рефлексивність: t = t ; Sm ) cиметричність: s = t t = s ; Tr ) транзитивність: s = t t = h s = h ; Теорема (еквiвалентостi). Нехай ‘ отримана iз формули замiною деяких входжень формул 1 , . . . , n на 1 , . . . , n. Якщо |= 1 1 , . . . , |= n n , то |= ‘. Теорема (рівності для термів). Нехай ‘ отриманийзтерма замiною деякихвходженьтермів s 1 , . . . , s n на t 1 , . . . , t n. Якщо |= s 1 = t 1 , . . . , |= s n = t n , то |= = ‘. Теорема (рівності для формул). Нехай ‘ отримана з формули замiноюдеяких входженьтермів s 1 , . . . , s n на t 1 , . . . , t n. Якщо |= s 1 = t 1 , . . . , |= s n = t n , то |= ‘. 1 1, . . . 1 1 1 1 ET) |= &. . . & ( , , . . . , )n nv v n n n nt s S t t t S t s s 1 1, . . . 1 1 1 1 E ) |= &. . . & ( ( , , . . . , ))n nv v n n n nt s S t t S s s

35Ім’я x V неiстотнедляформули , якщо A = ( A , I ) x неiстотне для A. Ім’я x V неiстотнедлятерма , якщо A = ( A , I ) x неiстотне для A. Критерії неістотності предметних імен для формул та термів: Теорема. Ім’я x V неістотнедля |= x Теорема. Ім’я х V неістотнедля у ( = S x ( , ‘y )). Звідси х V неістотне для формули x . Ім’я x тотальнонеістотне , якщо воно неiстотне для g Fп s Ps. Надалі розглядаємо такі інтерпретації, для яких виділена нескінченна підмножина V Т V тотально неістотних імен.

36 g F s Ps множину синтетичнонеістотних предметних імен визначимо за допомогою тотальної : Fs Ps 2 V. При цьому ‘x Dns ( ‘x ) = V \{ x }. Продовжимо таку функцію до : Tr Fr 2 V так: ( = ts ) = ( t ) ( s ) ( ) = ( ) ( ) ( x ) = ( ) { x } Пару ( F s Ps , ) назвемо сигнатурою синтетичної неістотності. Множина тотально неістотних імен мусить бути нескінченною Семантичною основою ФЕНКЛ є КС еквітонних функцій та предикатів з додатковою вимогою наявності нескінченної множини тотально неістотних предметних імен. 1, . . . , 1 1 { | ( )} (. . . ) ( ( ) { , . . . , }) ( )n i v v n n i i v t S t t v v t II ( )T g Fns Ps V g I

37 Теорема. 1) Нехайх ( ). Тодіхнеістотнедлятерма 2) Нехайх ( ). Тодіхнеістотнедляформули Наслідок. 1) Якщо x ( ), то у ( = Sx ( , ‘ y ). 2) Якщо x ( ), то x та х . Теорема. Нехай х ( g ) g ( F) тах fr (F). Тоді х ( ). В силу fr ( ) dn т ( ) і з х dn т ( ) випливає х fr ( ). Тому Наслідок 1. Нехай х ( g ) g ( ) та х dn m ( ). Тоді х ( ). Наслідок 2. Нехай х V тотальнонеістотне та х dn m ( ). Тоді х ( ). Ψ – варіанта формули Ξ, якщо Ψ утворена із Ξ послідовними замінами підформул х на підформули у S x ( , ‘ y ) при у ( ). Теорема (про варіанту). Нехай Ψ варіантаформули Ξ. Тоді Ψ Ξ.

38 Нормальні форми в ФЕНКЛ Формула Ψ знаходиться в різнокванторнійформі , якщо: – всі входження кв. префіксів у Ψ по різних тотально неіст. іменах; – підформули вигляду якщо А містить х , то Формула Ψ знаходиться в нормальнійформі (або НФ) якщо : – всі вх-ня квант. префіксів у Ψ по різних тотально неістотних іменах; – всі символи суперпозиції формули Ψ застосовні тільки до ФС чи ПС. Неважко переконатись, що кожна нормальна формула є різнокваторною. Терм мови ФЕНКЛ нормальний , якщо – всі його символи суперпозиції застосовані тільки до ФС – згорнуті неістотні імена і виконані спрощення згідно SST, ZNT, ZT, DS, DD Нормальна формула ФЕНКЛ стандартн a , якщо – для її термів та підформул згорнуті неістотні імена – виконані спрощення згідно ZN Ф, Z Ф та всі її терми нормальні. ( , )v S A t{ } та ( )x v x t

39 Теорема. формули можназбудуватирізнокванторну : . входженню кванторного префіксу х в c кладі підформули х А зіставимо тотально неістотне у (А): у nd n ( ) та різним входженням кванторних префіксів зіставлені різні тотально неістотні імена. Зрозуміло, що всі такі імена неістотні для кожного терма формули . Просуваючись по зліва направо, замінимо підформулу вигляду х А на у S x (А, ‘ y ), де у тотально неістотне, зіставлене такому входженню х в формулу . Отримаємо варіанту формули – різнокванторну Згідно х А у S x (А, ‘ y ) за теоремою еквівалентності Φ Теорема. ф-ли можназбудувати стандартнунормальну : . За будуємо різнокванторну ф-лу як описано вище. Маємо Φ . Використовуючи S , SE , а також SSФ та SSТ, проносимо всі символи c уперпозиції , згортаючи їх при потребі, вглиб формули до рівня ФС та ПС. Для спрощення використовуємо DD , DS , ZNT, ZN Ф, Z Ф. Отриму є мо : Ψ . Така нормальна, а згідно Φ та Ψ маємо Φ НФ , отримана із даної Ф описаним способом – нормалізанта ф-ли . Наслідок. Нехай нормалізантаформули Тоді .

40 Теорема. можназбудуватинормальнуквазізамкнену : . За спочатку будуємо різнокванторну формулу так, як описано вище. Якщо fr ( )= , далі будуємо формулу так, як описано вище. Позаяк fr ( ) = fr (Ψ) , то – квазізамкнена, вона є нормалізантою ф-ли , тому . Звідси . Нехай тепер fr ( ) = { u 1 , . . . , u k } ≠ . Маємо Φ . Візьмемо множину { у 1 , . . . , у k } тотально неістотних імен: { у 1 , . . . , у k } n dn ( ) = . Всі у 1 , . . . , у k ( ), тому Звідси Використ-чи S , SST, SS , проносимо всі символи cуперпозиції вглиб формули до рівня ПС та ФС. Отримуємо таку, що 1 . Тоді fr ( )= , всі вх — ня квант. префіксів в по різних тотально неістотних іменах, причому всі її ДНС ‘у такі, що у тотально неістотне Отже, квазі замкнена нормальна. Згідно , 1 та 1 маємо Отримана таким способом – квазізамкненанормалізанта формули . Наслідок. Нехай квазізамкнена норм-таф-ли Тоді . 1, . . . , 1 1 1|. . . ( , ‘ , . . . , ‘ )ku u k k ku u y y S y y 1, . . . , 1 1| | , де — це . . . ( , ‘ , . . . , ‘ )ku u k ky y S y y