1 Ізоморфне вкладення графів Лекція 10 Теорія графів

1 Ізоморфне вкладення графів Лекція 10 Теорія графів

2 Ізоморфне вкладення графів Ізоморфне вкладення та подовження графів Нехай G = (X, F) і H = (Y, P) – два довільних графи Бержа. Граф G = (X, F) ізоморфно вкладається у граф H = (Y, P) або граф H = (Y, P) та є ізоморфним подовженням графа G = (X, F), якщо множина X еквівалентна деякій підмножині Y'Y і для будь-яких елементів xX та yY', між якими встановлено бієктивне відображення, виконується умова Fx еквівалентно P'y, де P'yPyY'. Вважатимемо, що задано два графи G = (X, F) і H = (Y, P), які мають множини елементів X = {xi}, iI, I = {1, 2, ..., m} і Y = {yj}, jJ = {1, 2, ..., n}, mn; si і vj – напівстепені виходу, а pi і wj – напівстепені входу вершин xiX та yjY, відповідно.

3 Ізоморфне вкладення графів Лема 3.3. Якщо граф G = (X, F) ізоморфно вкладається у граф H = (Y, P), то існує принаймні одна підстановка tT, де T – симетрична група підстановок множини елементів порядку m!, яка визначає ін'єктивне відображення множини X графа G = (X, F) у множину Y графа H = (Y, P) таке, що (xiX)(yjY)[(sivj)(piwj)]. Лема 3.4. Якщо існує підстановка tT множини вершин X графа G(X, F) на множину Y' графа H'H, що переводить граф G = (X, F) у граф H' = (Y', P), то граф G = (X, F) ізоморфно вкладається у граф H = (Y, P). Доведення леми випливає із означення ізоморфного вкладення графів. Леми про ізоморфне вкладення графів

4 Ізоморфне вкладення графів Теорема про ізоморфне вкладення графів Теорема 3.3. Для того, щоб граф G = (X, F) ізоморфно вкладався у граф H = (Y, P), необхідно та достатньо виконання наступних умов: а) (xiX)(yjY)[(sivj)(piwj)] (для кожної вершини xiX графа G = (X, F) має існувати принаймні одна така вершина yjY у графі H = (Y, P)); б) tT множини X у множину Y'Y така, що переводить граф G = (X, F) у граф H' = (Y', P), причому H'H. Необхідність випливає із леми 3.3, а достатність – із леми 3.4.

5 Ізоморфне вкладення графів Алгоритм розпізнавання ізоморфного вкладення графа G = (X, F) у граф H = (Y, P)

6 Ізоморфне вкладення графів Кроки алгоритму (1) Алгоритм має такі кроки: 1. Підраховуємо кількість вершин m графа G = (X, F) і n графа H = (Y, P). Якщо mn, то переходимо до п. 2, в іншому випадку – до п. 9. 2. Виписуємо всі вершини обох графів G = (X, F) і H = (Y, P) у природній упорядкованості з відношеннями кожної з них, визначаємо пари (s, p) і (v, w) для кожної вершини xX та yY. 3. Перевіряємо виконання умови а теореми 3.3. Якщо вона виконується, то переходимо до п. 4, у протилежному випадку – до п. 9. 4. Вершині xiX графа G = (X, F) з максимальним числом si зіставляємо таку вершину yjY графа H = (Y, P), для якої виконується умова а теореми 3.3.

7 Ізоморфне вкладення графів Кроки алгоритму (2) 5. Кожній вершині xlFxi ставимо у взаємно однозначну відповідність одну із вершин ykPyj так, щоб виконувалась умова а теореми 3.3. Одержуємо часткову підстановку t1 множини X на Y'Y. Переходимо до п. 7. Якщо умова а теореми 3.3 для вершин xl та yk не виконується, то переходимо до п. 6. 6. Вершині xiX графа G = (X, F) із максимальним числом si зіставляємо другу вершину ylY графа H = (Y, P), для якої виконується умова а теореми 3.3. Переходимо до п. 5. Якщо такої вершини не знайдено, то переходимо до п. 9.

8 Ізоморфне вкладення графів Кроки алгоритму (3) 7. Використовуємо часткову підстановку t1 і перевіряємо її для останніх m–1 вершин графа G = (X, F). Якщо підстановка t1 не суперечить відношенням елементів yY, то довизначаємо її для останніх елементів множини X, що не входять до часткової підстановки t1. Одержуємо підстановку tT множини X на множину Y'Y. Переходимо до п. 8. Якщо знайдену часткову підстановку неможливо довизначити, то переходимо до п. 5 і встановлюємо нову відповідність між вершинами xl та yk. 8. Граф G = (X, F) ізоморфно вкладається у граф H = (Y, P). 9. Граф G = (X, F) ізоморфно не вкладається у граф H = (Y, P).

9 Ізоморфне вкладення графів Випадок mn Якщо mn, то можна використовувати цей алгоритм для розпізнавання ізоморфного вкладення графа H = (Y, P) у граф G = (X, F). Коли m = n, можливі такі випадки: граф G = (X, F) ізоморфно вкладається у граф H = (Y, P); граф H = (Y, P) ізоморфно вкладається у граф G = (X, F); граф G = (X, F) ізоморфно вкладається у граф H = (Y, P), а граф H = (Y, P) ізоморфно вкладається у граф G = (X, F), тобто графи G = (X, F) і H = (Y, P) ізоморфні; графи G = (X, F) і H = (Y, P) ізоморфно не вкладаються один до одного.

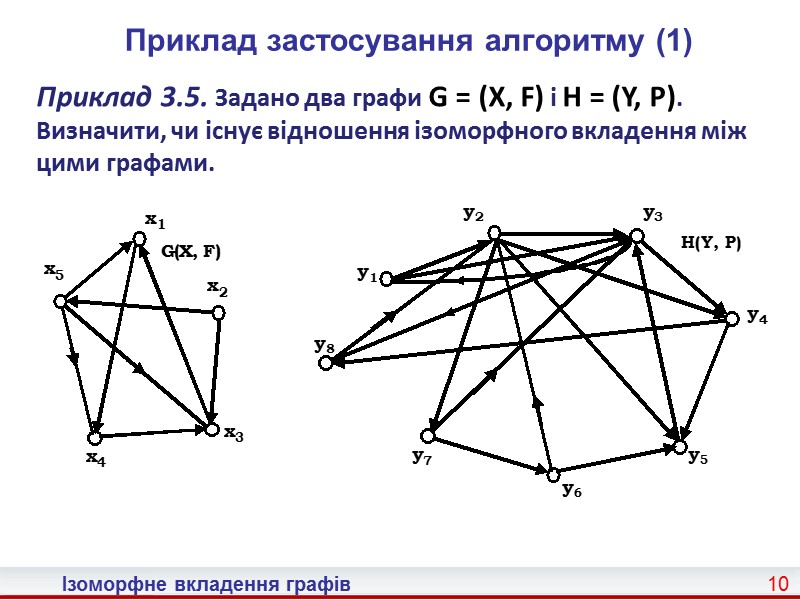
10 Ізоморфне вкладення графів Приклад застосування алгоритму (1) Приклад 3.5. Задано два графи G = (X, F) і H = (Y, P). Визначити, чи існує відношення ізоморфного вкладення між цими графами.

11 Ізоморфне вкладення графів Приклад застосування алгоритму (1) Виконуємо послідовно пункти алгоритму. 1. Оскільки кількість вершин графа G = (X, F) менша за кількість вершин графа H = (Y, P), шукатимемо ізоморфне вкладення графа G = (X, F) у граф H = (Y, P). 2. Випишемо вершини графів G = (X, F) і H = (Y, P) у природному порядку з відношеннями кожної із них і парами (s, p) та (v, w). В результаті одержимо (слайд 12):

12 Ізоморфне вкладення графів Приклад застосування алгоритму (2) Вершини графів і у природному порядку з відношеннями кожної із них і парами (s, p) та (v, w).

13 Ізоморфне вкладення графів Приклад застосування алгоритму (3) 3. Умова а теореми 3.3 для графів G = (X, F) і H = (Y, P) виконується. 4. Вершині x5 графа G = (X, F) із максимальною кількістю виходів можна зіставити тільки вершини y2 та y3 графа H = (Y, P), оскільки для інших вершин умова а теореми 3.3 не виконується. Але й для множин Fx5 і Py3 також не виконується ця умова. Тому вершині x5 ставимо у відповідність вершину – y2.

14 Ізоморфне вкладення графів Приклад застосування алгоритму (4) 5. Із зіставлення множин Fx5 і Py2 візьмемо часткову підстановку t1= так, щоб для її елементів виконувалась умова а теореми 3.3. 6. Перевіримо одержану часткову підстановку для інших вершин графа G = (X, F). Видно, що у графі G = (X, F) відношення Fx1 = {x4}. Із підстановки t1 випливає, що Py3 має включати y5, що не відповідає дійсності. Таким чином, необхідно взяти іншу часткову підстановку t2.

15 Ізоморфне вкладення графів Приклад застосування алгоритму (5) 7. Вибираємо t2 = для елементів якої також виконується умова а теореми 3.3. Перевіряємо підстановку t2 для вершин x1, x3, x4. Підстановка t2 не суперечить відношенням елементів y3, y4, y5, а тому довизначаємо її у такий спосіб: із зіставлення відношень Fx2 і Py6 встановлюємо відповідність між вершинами x2 та y6.

16 Ізоморфне вкладення графів Приклад застосування алгоритму (6) 8. Отримуємо підстановку t множини X на множину Y'Y такого вигляду t= 9. Підстановка показує, що граф G = (X, F) ізоморфно вкладається у граф H = (Y, P).

17 Ізоморфне вкладення графів Теоретико-множинні операції над графами До теоретико-множинних операцій над графами належать: об'єднання; переріз; доповнення за відношенням; різниця, сполучення; диз'юнктивна сума.

18 Ізоморфне вкладення графів Алгебраїчні операції над графами До алгебраїчних операцій над графами належать такі: добутку; підсумовування; композиції; суперпозиції.

19 Ізоморфне вкладення графів Розкладання графів за теоретико-множинними та алгебраїчними операціями Важливою проблемою теорії графів є розкладання складних графів на простіші за різними операціями. Методи розкладання графів використовуються для декомпозиції скінченних автоматів. Найчастіше розкладання графів виконується за двома операціями: теоретико-множинною (об'єднання або переріз) та алгебраїчною (добуток або композиція). Основні операції розкладання графів: у добуток двох графів G' = G  H; у суму двох графів G' = G + H; за операцією суперпозиції; в об'єднання добутків графів; за операцією композиції тощо.

20 Ізоморфне вкладення графів