1 1 1 Алгоритмы и структуры данных Сортировки

1 1 1 Алгоритмы и структуры данных Сортировки ЛЕКЦИЯ 4 Валенда Н.А. Кафедра Программной инженерии, факультет КН, ХНУРЕ

2 2 Сортировки Быстрая сортировка Сортировка подсчетом Цифровая сортировка

3 3 Быстрая сортировка Алгоритм разработан Чарльзом Хоаром в 1960 г. Разделяем массив на два подмассива [1 ...m] и [m +1 . ..N], причем 2. Рекурсивно сортируем получившиеся два подмассива. Быстрая сортировка использует стратегию Разделяй и властвуй Выбираем в массиве некоторый элемент, который будем называть опорным элементом. Известные стратегии: выбирать постоянно один и тот же элемент, например, первый, средний или последний по положению; выбирать элемент со случайно выбранным индексом.

4 Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него. Два индекса — l и r, приравниваются к минимальному и максимальному индексу разделяемого массива соответственно. Вычисляется индекс опорного элемента m. Индекс l последовательно увеличивается до тех пор, пока l-й элемент не превысит опорный. Индекс r последовательно уменьшается до тех пор, пока r-й элемент не окажется меньше либо равен опорному. Если r = l — найдена середина массива — операция разделения закончена, оба индекса указывают на опорный элемент. Если l < r — найденную пару элементов нужно обменять местами и продолжить операцию разделения с тех значений l и r, которые были достигнуты. Рекурсивно упорядочиваем подмассивы, лежащие слева и справа от опорного элемента. Базой рекурсии являются наборы, состоящие из одного или двух элементов. Первый возвращается в исходном виде, во втором, при необходимости, сортировка сводится к перестановке двух элементов. Все такие отрезки уже упорядочены в процессе разделения.

5 Алгоритм быстрой сортировки Quicksort (int A[], int p, int r){ if (l <= r){ int q = Partition(A, p, r) Quicksort(A, p, q - 1) Quicksort (A, q + 1, r) }

6 Алгоритм разделения в быстрой сортировке Partition ( A, p, r) 1 x ←A[r] 2 i ← p - 1 3 for j ← p to r - 1 4 do if A[j] ≤ x 5 then i ← i +1 6 Обменять A[i] ↔ A[j] 7 Обменять A[i +1] ↔ A[r] 8 return i+1

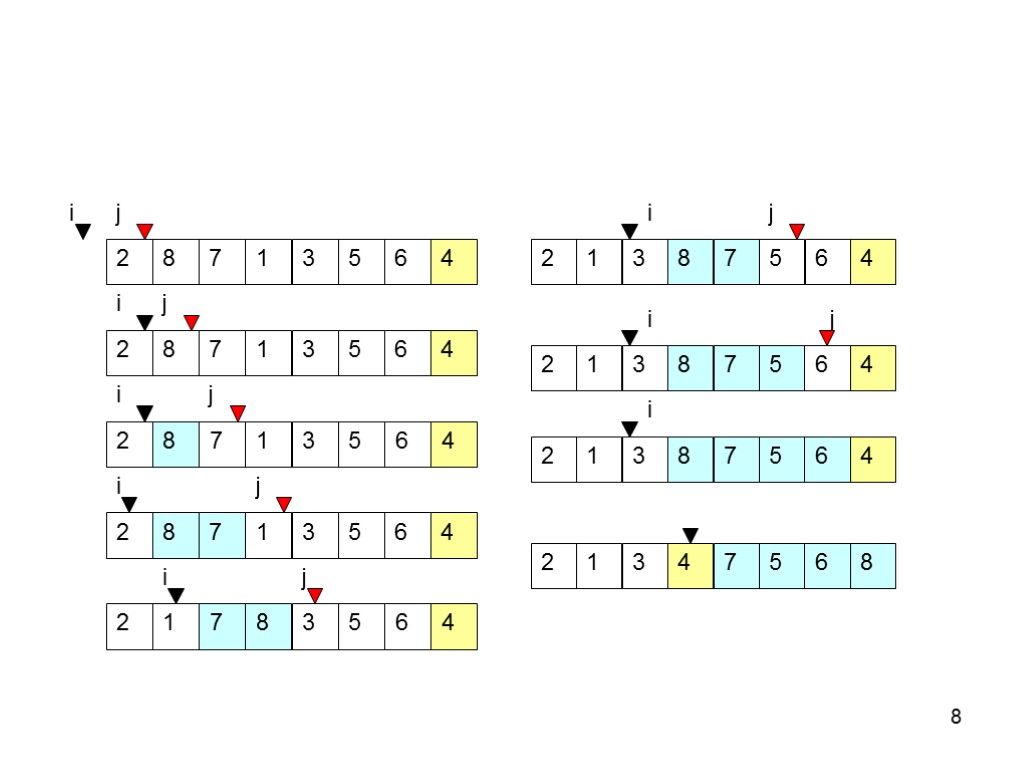
7 Разбиение массива на части в Partition если p<=k<=i, A[k]<=x если i+1<=k<=j-1, A[k]>x если k=r, A[k]=x

8

9 Алгоритм разделения в быстрой сортировке int Partition (int A[], int left, int right) int s= left++; while(left<=right){ while(A[left]=A[s]) --right; if (left

10 Алгоритм быстрой сортировки на С++ void quicksort (int а[], int l, int г) { int x, w; int i , j ; i = 1; j = r; x = a[(l + r)/2]; do { while (a[i] < x) i++; while (x < a[j]) j--; if (i <= j) { w = a[i] ; a [i] = a [j] ; a[j] = w; i++; j--; } } while (i<=j); if (l < j) quicksort (a, l, j); if (i < r) quicksort (a, i, r); }

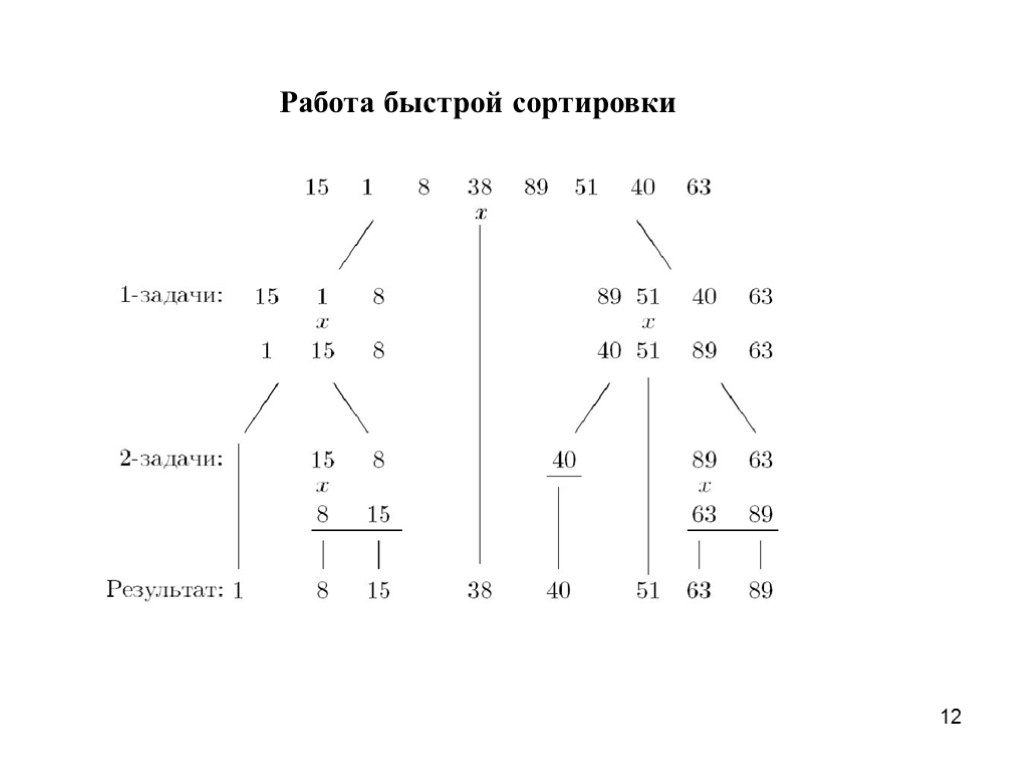
11 Работа быстрой сортировки

12 Работа быстрой сортировки

13 Анализ быстрой сортировки (наихудший случай) Предположим, что все элементы различны. Наихудший случай: когда при разделении один из массивов не имеет элементов. T(n) = T(0) + T(n - 1) + Θ(n) = Θ(1) + T(n - 1) + Θ(n) = T(n - 1) + Θ(n) = Θ(n2)

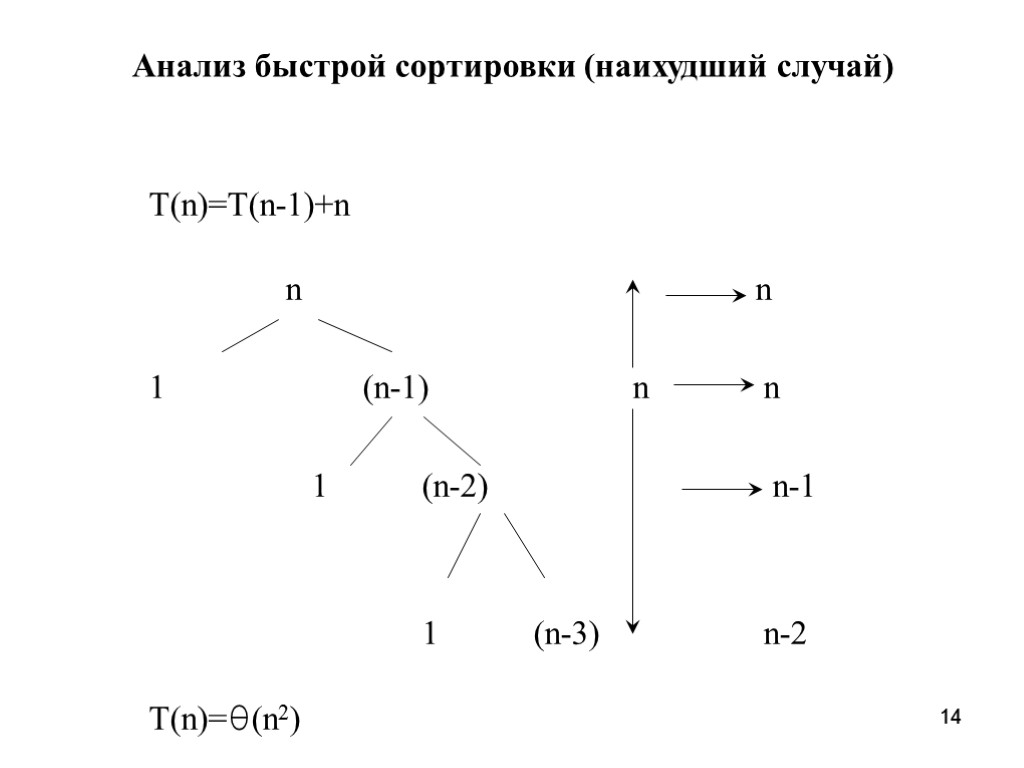
14 14 Анализ быстрой сортировки (наихудший случай) T(n)=T(n-1)+n n n 1 (n-1) n n 1 (n-2) n-1 1 (n-3) n-2 T(n)=θ(n2)

15 Анализ быстрой сортировки (наилучший случай) Наилучший случай: когда при разделении массив разделяется на равные части. Т(n) = 2T (n/2) + Θ(n) = Θ(n • log(n))

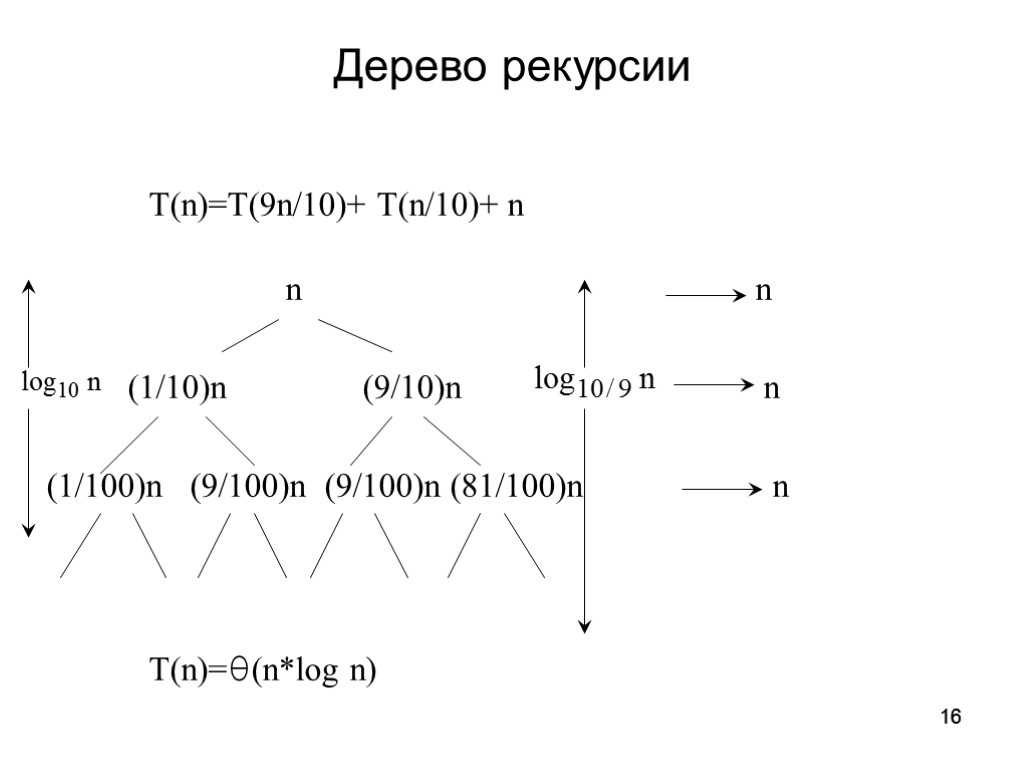
16 16 Дерево рекурсии T(n)=T(9n/10)+ T(n/10)+ n n n (1/10)n (9/10)n n (1/100)n (9/100)n (9/100)n (81/100)n n T(n)=θ(n*log n)

17 Рандомизированная быстрая сортировка Время работы не зависит от порядка элементов во входных данных; Не нужно предположений о распределении входных данных; Нет входных данных, которые приводят к наихудшему случаю; Наихудший случай определяется только генератором случайных чисел.

18 Рандомизированная быстрая сортировка Выбираем граничный элемент случайным образом! RandomizedPartition (A,p,r) 1 i ← Random(p,r) 2 Обменять A[r] ↔ A[i] 3 return Partition(A,p,r) RandomizedQuickSort(A,p, r) 1 if p < r 2 then q ← RandomizedPartition(A, p, r) 3 RandomizedQuicksort(A,p,q - 1) 4 RandomizedQuicksort(A, q + 1, r)

19 Наименьшее время сортировки Теорема. В любом алгоритме, упорядочивающем с помощью сравнения пар, на упорядочивание последовательности из N элементов тратится не меньше c * N * log2N сравнений при c = 0 и N → ∞. T(n) > c • N • log2N, при c = 0 и N → ∞

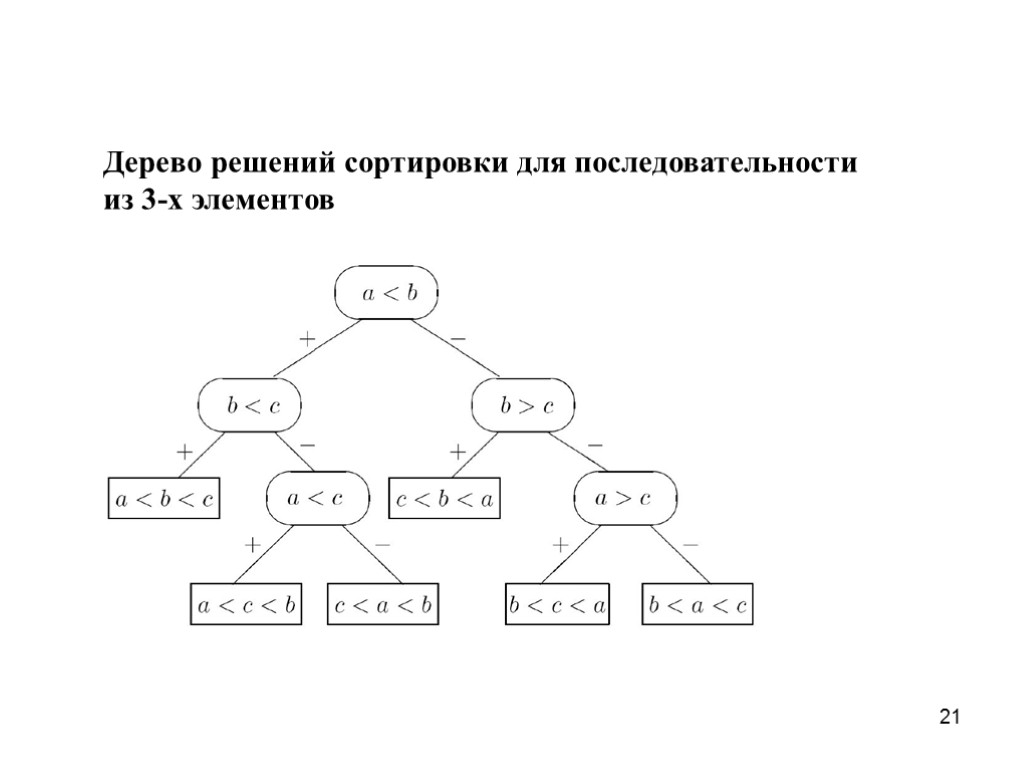
20 Наименьшее время сортировки. Доказательство Число перестановок последовательности из N элементов равно N! Сортировка путем сравнения пар есть спуск по дереву решений – двоичному, где листья перестановки, а внутренние узлы условия. Число сравнений равно высоте разрешающего дерева

21 Дерево решений сортировки для последовательности из 3-х элементов

22 Число листьеа N! Двоичное дерево высоты h имеет не более 2h листьев N! ≤ 2h

23 Сортировка за линейное время. Сортировка подсчетом Все n входных элементов - целые числа, принадлежащие [0,k], где k - целая константа. Если k = O(n), то T(n) = Θ(n)

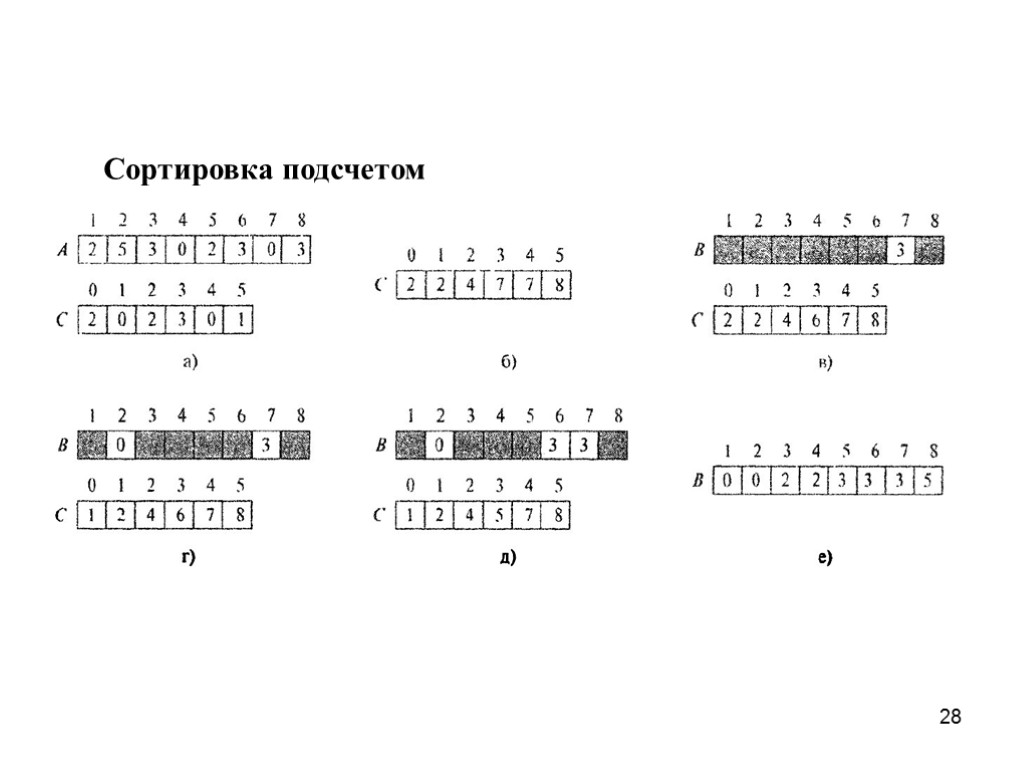
24 Сортировка подсчетом Исходная последовательность чисел длины n, в конце отсортированная, хранится в массиве A. Также используется вспомогательный массив C с индексами от 0 до k-1 , изначально заполняемый нулями. Последовательно пройдём по массиву A и запишем в C[i] количество чисел, равных i . Теперь достаточно пройти по массиву C и для каждого number в массив A последовательно записать число number C[number] раз.

25 Сортировка подсчетом

26 Сортировка подсчетом Сортировка просто целых чисел за линейное время это хорошо, но недостаточно. Иногда бывает очень желательно применить быстрый алгоритм сортировки подсчетом для упорядочивания набора каких-либо "сложных" данных. Под "сложными объектами" здесь подразумеваются структуры, содержащие в себе несколько полей. Одно из них мы выделим и назовем ключом, сортировка будет идти именно по нему (предполагается, что значения, принимаемые ключом — целые числа в диапазоне от 0 до k-1 ). Мы не сможем использовать здесь в точности тот же алгоритм, что и для сортировки подсчетом обычных целых чисел, потому что в наборе могут быть различные структуры, имеющие одинаковые ключи. Идея алгоритма состоит в предварительном подсчете количества элементов с различными ключами в исходном массиве и разделении результирующего массива на части соответствующей длины (будем называть их блоками). Затем при повторном проходе исходного массива каждый его элемент копируется в специально отведенный его ключу блок.

27 Сортировка подсчетом Исходная последовательность записана в массиве А Отсортированная в массиве В CountingSort(A, B, k) 1 for i ← 0 to k 2 do C [i] ← 0 3 for j ← 1 to length[A] 4 do C[A[j]] ← C[A[j]] + 1 5 ► B C[i] хранится количество элементов равных i 6 for i ← 1 to k 7 do C [i] ← C[i] + C [i - 1] 8 ► В C[i] хранится количество элементов не превышающих i for j ← length [A] downto 1 do B[C[A[j]]] ← A[j] 11 C[A[j]] ← C[A[j]] - 1

28 Сортировка подсчетом

29 Анализ сортировки подсчетом Т(n) = 2*О(k)+ 2*O(n) = Θ(n), если k=O(n)

30 Сортировка за линейное время. Цифровая сортировка По аналогии с разрядами чисел будем называть элементы, из которых состоят сортируемые объекты, разрядами. Сам алгоритм состоит в последовательной сортировке объектов какой-либо устойчивой сортировкой по каждому разряду, в порядке от младшего разряда к старшему, после чего последовательности будут расположены в требуемом порядке. Примерами объектов, которые удобно разбивать на разряды и сортировать по ним, являются числа и строки. Для чисел уже существует понятие разряда, поэтому будем представлять числа как последовательности разрядов. Строки представляют из себя последовательности символов, поэтому в качестве разрядов в данном случае выступают отдельные символы, сравнение которых обычно происходит по соответствующим им кодам. Для такого разбиения самый младший разряд — последний символ строки. Для вышеперечисленных объектов наиболее часто в качестве устойчивой сортировки применяют сортировку подсчетом.

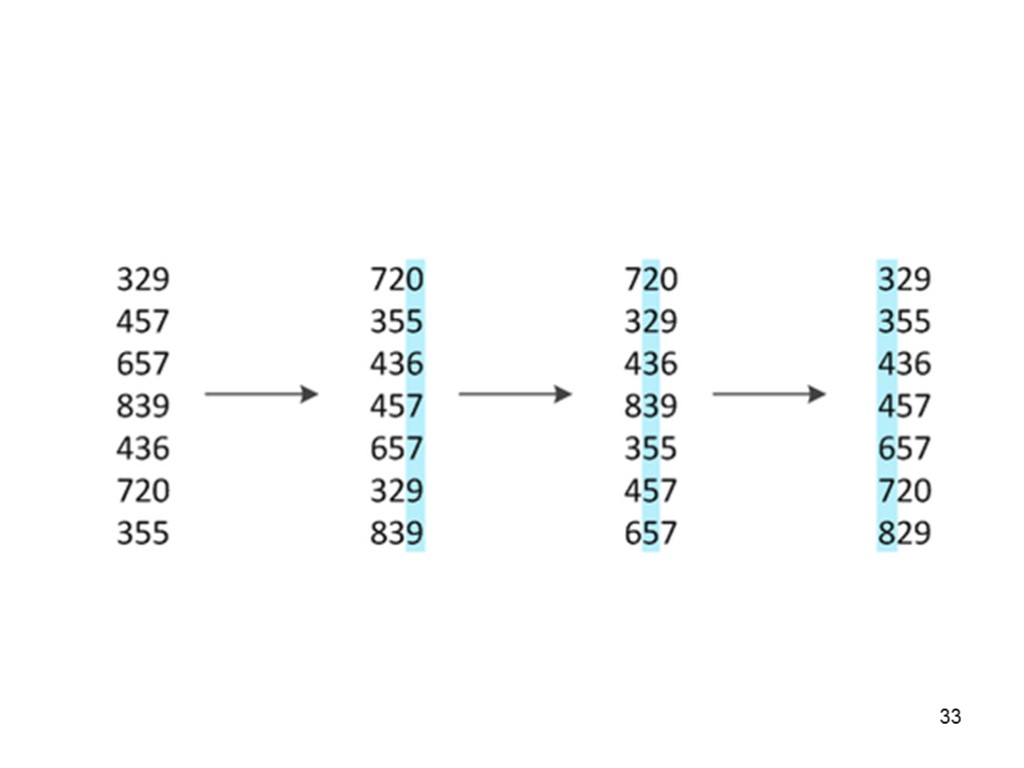
31 Цифровая сортировка Рассмотрим сортировку чисел. В качестве устойчивой сортировки применяют сортировку подсчетом, так как обычно количество различных значений разрядов не превосходит количества сортируемых элементов. Ниже приведен псевдокод цифровой сортировки, которой подается массив A m-разрядных чисел размера n. Сам по себе алгоритм представляет собой цикл по номеру разряда, на каждой итерации которого элементы массива размещаются в нужном порядке во вспомогательном массиве B. Для подсчета количества объектов, i-й разряд которых одинаковый, а затем и для определения положения объектов в массиве B используется вспомогательный массив C. Функция digit(x,i) возвращает i-й разряд числа х. Также считаем, что значения разрядов меньше k.

32 Цифровая сортировка

33

34 Анализ сложности. Цифровая сортировка Пусть в качестве аргумента сортировке передается массив, в котором содержатся n m-значных чисел, и каждая цифра может принимать значения от 0 до k-1 . Цифровая сортировка позволяет отсортировать данный массив за время O(m*(n+k)), если устойчивая сортировка имеет время работы O(n+k) . Если k небольшое, то оптимально выбирать в качестве устойчивой сортировки сортировку подсчетом. Если количество разрядов — константа, а k=O(n), то сложность цифровой сортировки составляет O(n), то есть она линейно зависит от количества сортируемых чисел.